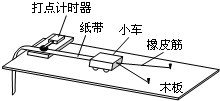
(2011?海淀区一模)(1)“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W
0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W
0、3W
0、4W
0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.关于该实验,下列说法正确的是
AC
AC
A.某同学在一次实验中,得到一条记录纸带.纸带上打出的点,两端密、中间疏.出现这种情况的原因,可能是没有使木板倾斜或倾角太小.
B.当小车速度达到最大时,橡皮筋处于伸长状态,小车在两个铁钉的连线处
C.应选择纸带上点距均匀的一段计算小车的最大速度
D.应选择纸带上第一点到最后一点的一段计算小车的最大速度.
(2)某兴趣小组在做“探究做功和物体速度变化关系”的实验前,提出了以下几种猜想:①W∝v,②W∝v
2,③W∝
.他们的实验装置如图甲所示,PQ为一块倾斜放置的木板,在Q处固定一个速度传感器(用来测量物体每次通过Q点的速度).在刚开始实验时,有位同学提出,不需要测出物体质量,只要测出物体初始位置到速度传感器的距离和读出速度传感器的读数就行了,大家经过讨论采纳了该同学的建议.
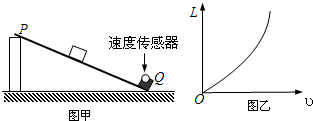
①请你简要说明为什么不需要测出物体的质量?
②让小球分别从不同高度无初速释放,测出物体初始位置到速度传感器的距离L
1、L
2、L
3、L
4…,读出小球每次通过Q点的速度v
1、v
2、v
3、v
4、…,并绘制了如图乙所示的L-v图象.若为了更直观地看出L和v的变化关系,他们下一步应怎么做?
(3)某同学要测量一均匀新材料制成的圆柱体的电阻率ρ.步骤如下:
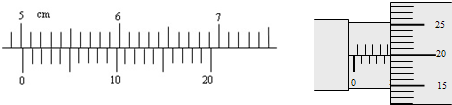
①用游标为20分度的卡尺测量其长度如图,由图可知其长度为
50.15
50.15
mm;
②用螺旋测微器测量其直径如右上图,由图可知其直径为
4.700
4.700
mm;
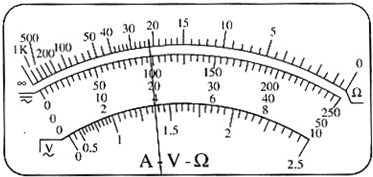
③用多用电表的电阻“×10”挡,按正确的操作步骤测此圆柱体的电阻,表盘的示数如图,则该电阻的阻值约为
220
220
Ω.

④该同学想用伏安法更精确地测量其电阻R,现有的器材及其代号和规格如下:
待测圆柱体电阻R
电流表A
1(量程0~4mA,内阻约50Ω)
电流表A
2(量程0~10mA,内阻约30Ω)
电压表V
1(量程0~3V,内阻约10kΩ)
电压表V
2(量程0~15V,内阻约25kΩ)
直流电源E(电动势4V,内阻不计)
滑动变阻器R
1(阻值范围0~15Ω,允许通过的最大电流2.0A)
滑动变阻器R
2(阻值范围0~2kΩ,允许通过的最大电流0.5A)
开关S
导线若干
为使实验误差较小,要求测得多组数据进行分析,请在右框中画出测量的电路图,并标明所用器材的代号.
⑤若该同学用伏安法跟用多用电表测量得到的R测量值几乎相等,由此可估算此圆柱体材料的电阻率约为ρ=
7.6×10-2
7.6×10-2
Ω?m.(保留2位有效数字)

 (2011?海淀区一模)在高能物理研究中,粒子加速器起着重要作用,而早期的加速器只能使带电粒子在高压电场中加速一次,因而粒子所能达到的能量受到高压技术的限制.1930年,Earnest O.Lawrence提出了回旋加速器的理论,他设想用磁场使带电粒子沿圆弧形轨道旋转,多次反复地通过高频加速电场,直至达到高能量.图甲为Earnest O.Lawrence设计的回旋加速器的示意图.它由两个铝制D型金属扁盒组成,两个D形盒正中间开有一条狭缝;两个D型盒处在匀强磁场中并接有高频交变电压.图乙为俯视图,在D型盒上半面中心S处有一正离子源,它发出的正离子,经狭缝电压加速后,进入D型盒中.在磁场力的作用下运动半周,再经狭缝电压加速;为保证粒子每次经过狭缝都被加速,应设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致.如此周而复始,最后到达D型盒的边缘,获得最大速度后被束流提取装置提取出.已知正离子的电荷量为q,质量为m,加速时电极间电压大小恒为U,磁场的磁感应强度为B,D型盒的半径为R,狭缝之间的距离为d.设正离子从离子源出发时的初速度为零.
(2011?海淀区一模)在高能物理研究中,粒子加速器起着重要作用,而早期的加速器只能使带电粒子在高压电场中加速一次,因而粒子所能达到的能量受到高压技术的限制.1930年,Earnest O.Lawrence提出了回旋加速器的理论,他设想用磁场使带电粒子沿圆弧形轨道旋转,多次反复地通过高频加速电场,直至达到高能量.图甲为Earnest O.Lawrence设计的回旋加速器的示意图.它由两个铝制D型金属扁盒组成,两个D形盒正中间开有一条狭缝;两个D型盒处在匀强磁场中并接有高频交变电压.图乙为俯视图,在D型盒上半面中心S处有一正离子源,它发出的正离子,经狭缝电压加速后,进入D型盒中.在磁场力的作用下运动半周,再经狭缝电压加速;为保证粒子每次经过狭缝都被加速,应设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致.如此周而复始,最后到达D型盒的边缘,获得最大速度后被束流提取装置提取出.已知正离子的电荷量为q,质量为m,加速时电极间电压大小恒为U,磁场的磁感应强度为B,D型盒的半径为R,狭缝之间的距离为d.设正离子从离子源出发时的初速度为零.
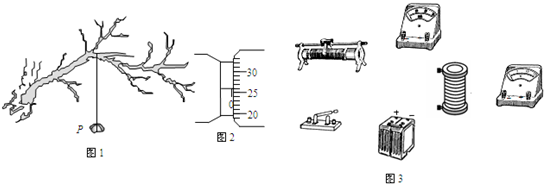
 (2011?海淀区一模)(1)“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W0、3W0、4W0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.关于该实验,下列说法正确的是
(2011?海淀区一模)(1)“探究动能定理”的实验装置如图所示,当小车在两条橡皮筋作用下弹出时,橡皮筋对小车做的功记为W0.当用4条、6条、8条…完全相同的橡皮筋并在一起进行第2次、第3次、第4次…实验时,橡皮筋对小车做的功记为2W0、3W0、4W0…,每次实验中由静止弹出的小车获得的最大速度可由打点计时器所打的纸带测出.关于该实验,下列说法正确的是


