练习册

  • 练习册
  • 试题
    12．如图所示.半径为R的半球支撑面顶部有一小孔．质量分别为m1和m2的两只小球.通过一根穿过半球顶部小孔的细线相连.不计所有摩擦．请你分析: (1)m2小球静止在球面上时.其平衡位置与半球面的球心连线跟水平方向的夹角为θ.则m1.m2.θ和R之间应满足什么关系, (2)若m2小球静止于θ＝45°处.现将其沿半球面稍稍向下移动一些.则释放后m2能否回到原来位置? [答案] (1)m1＝m2cosθ与R无关 (2)不能 [解析] (1)根据平衡条件有m2gcosθ＝m1g.所以m1＝m2cosθ(或cosθ＝).与R无关． (2)不能回到原来位置.m2所受的合力为m2gcosθ′-m1g＝m2g(cosθ′-cos45°)>0(因为θ′<45°).所以m2将向下运动． 【查看更多】

     

    题目列表(包括答案和解析)

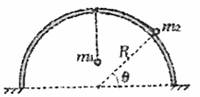
    如图所示，半径为R的半球支撑面顶部有一小孔，质量分别为m1和m2的两只小球（视为质点），通过一根穿过半球顶部小孔的细线相连，不计所有摩擦，请你分析

    （1）m2小球静止在球面上时，其平衡位置与半球面的球心连线跟水平方向的夹角为θ，则m1、m2，θ和R之间应满足什么关系；

    （2）若m2小球静止于θ=45°处，现将其沿半球面稍稍向下移动一些，则释放后m2能否回到原来位置？请作简析。

    查看答案和解析>>

    如图所示，半径为R的半球支撑面顶部有一小孔. 质量分别为m1和m2的两只小球（视为质点），通过一根穿过半球顶部小孔的细线相连，不计所有摩擦. 请你分析
    小题1:m2小球静止在球面上时，其平衡位置与半球面的球心连线跟水平方向的夹角为θ，则m1、m2、θ和R之间应满足什么关系；
    小题2:若m2小球静止于θ=45°处，现将其沿半球面稍稍向下移动一些，则释放后m2能否回到原来位置？请作简析。

    查看答案和解析>>

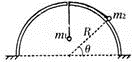
    如图所示http://www.ks5u.com，半径为R的半球支撑面顶部有一小孔. 质量分别为m1和m2的两只小球（视为质点），通过一根穿过半球顶部小孔的细线www.ks5u.com相连，不计所有摩擦. 请你分析

    m2小球静止在球面上时，其平衡位置与半球面的球心连线跟水平方向的夹角为θ，则m1、m2、θ和R之间应满足什么关系；

    若m2小球静止于θ=45°处，现将其沿半球面稍稍向下移动一些，则释放后m2能否回到原来位置？请作简析。

    查看答案和解析>>

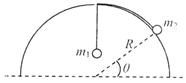
    （2012年5月山东省烟台二模）如图所示，半径为R的半球支撑面顶部有一小孔，质量分别为m1和m2的两个小球（视为质点），通过一根穿过半球顶部小孔的细线相连，不计所有的摩擦，当小球m2静止在球面上、其平衡位置与半球面的球心连线跟水平面的夹角为θ时，则m1、m2，、θ之间的关系为

    A． m1=m2sinθ　　　　　　　　　　　　　　　　　　　

    B．m1=m2/sinθ　　

    C．m1=m2cosθ　　　　　　　　　　　　　　　　　　　

    D．m1=m2/cosθ

    查看答案和解析>>

    在电视中我们常看见魔术师使圆筒在空中无任何支撑条件下运动，简称“魔环运动”，其原理如图1所示．即水平地面上竖直放置一个质量为m、半径为R的光滑金属圆筒，在圆筒最底点P安装一个储备一定能量的弹簧装置，将一质量为2m的小球A（可视为质点）置于P点，打开弹簧装置将弹簧储备的能量全部转移给A，A就会从圆筒的P点运动到最高点Q，又从Q点运动P点，在这一过程中，圆筒将离开地面时而向上或向下运动，这就是“魔环运动”．设筒的内径、弹簧装置的大小、圆筒自身的运动可以忽略，完成下列问题：
    （1）要使A要到达Q点，求A在P点的最小速度．
    （2）当A运动到Q点时，要使圆筒离开地面，求A在Q点的最小速度．
    （3）当A运动到Q点时，要使圆筒具有大小为g，方向竖直向上的加速，则弹射装置应该储备的能量？
    （4）以A在最高点对圆筒的作用力FN为纵坐标（规定向上为正），弹簧装置储备的能量E为横坐标，在图2中作出FN-E图象．
    精英家教网

    查看答案和解析>>


    同步练习册答案