
题目列表(包括答案和解析)
 如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点与一条水平轨道相连,轨道都是光滑的.轨道所在空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m的带正电的小球,为使小球刚好在圆轨道内做圆周运动,已知小球受到的电场力大小等于小球重力的
如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点与一条水平轨道相连,轨道都是光滑的.轨道所在空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m的带正电的小球,为使小球刚好在圆轨道内做圆周运动,已知小球受到的电场力大小等于小球重力的| 3 | 4 |
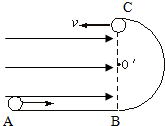 如图所示,一半径为R的绝缘圆形轨道竖直放置,BC为圆轨道的直径,圆轨道最低点与一条水平轨道相连.已知所有的轨道均为光滑的,水平轨道所在空间存在水平向右的匀强电场.从水平轨道上的A点由静止释放一质量为m,电量为q的带正电的小球,已知小球恰好能从A点运动2.5R的距离到达B点进入圆轨道,并恰能通过圆轨道的顶端C点.求:
如图所示,一半径为R的绝缘圆形轨道竖直放置,BC为圆轨道的直径,圆轨道最低点与一条水平轨道相连.已知所有的轨道均为光滑的,水平轨道所在空间存在水平向右的匀强电场.从水平轨道上的A点由静止释放一质量为m,电量为q的带正电的小球,已知小球恰好能从A点运动2.5R的距离到达B点进入圆轨道,并恰能通过圆轨道的顶端C点.求: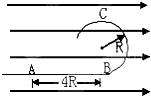 如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点与一条水平轨道相连,轨道都是光滑的,轨道所在空间存在水平向右的匀强电场,从水平轨道上的A点由静止释放一质量为m带正电的小球,释放点A距圆轨道最低点B的距离为4R,已知电场力大小等于小球重力的
如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点与一条水平轨道相连,轨道都是光滑的,轨道所在空间存在水平向右的匀强电场,从水平轨道上的A点由静止释放一质量为m带正电的小球,释放点A距圆轨道最低点B的距离为4R,已知电场力大小等于小球重力的| 3 | 4 |
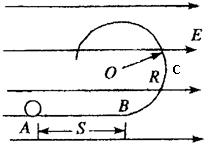 如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点B点与一条水平轨道相连,轨道都是光滑的,轨道所在空间存在水平向右、场强为E的匀强电场,从水平轨道上的A点由静止释放一质量为m带正电的小球,设A、B间的距离为S.已知小球受到的电场力大小等于小球重力的3/4倍,C点为圆形轨道上与圆心O的等高点.(重力加速度为g)
如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点B点与一条水平轨道相连,轨道都是光滑的,轨道所在空间存在水平向右、场强为E的匀强电场,从水平轨道上的A点由静止释放一质量为m带正电的小球,设A、B间的距离为S.已知小球受到的电场力大小等于小球重力的3/4倍,C点为圆形轨道上与圆心O的等高点.(重力加速度为g)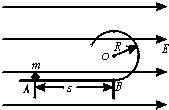 如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点与一条水平轨道相连,轨道都是光滑的.轨道所在空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m的带正电的小球,为使小球刚好在圆轨道内做圆周运动,求释放点A距圆轨道最低点B的距离s.已知小球受到的电场力大小等于小球重力的
如图所示,一半径为R的绝缘圆形轨道竖直放置,圆轨道最低点与一条水平轨道相连,轨道都是光滑的.轨道所在空间存在水平向右的匀强电场,场强为E.从水平轨道上的A点由静止释放一质量为m的带正电的小球,为使小球刚好在圆轨道内做圆周运动,求释放点A距圆轨道最低点B的距离s.已知小球受到的电场力大小等于小球重力的| 3 | 4 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com