
题目列表(包括答案和解析)
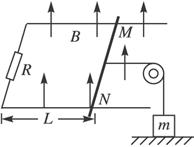
图15
如图(12)所示,挡板P固定在足够高的水平桌面上,小物块A和B大小可忽略,它们分别带有+QA和+QB的电荷量,质量分别为mA和mB。两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过滑轮,一端与B连接,另一端连接一轻质小钩.整个装置处于场强为E、方向水平向左的匀强电场中。A、B开始时静止,已知弹簧的劲度系数为k,不计一切摩擦及A、B间的库仑力,A、B所带电荷量保持不变,B不会碰到滑轮。
(1)若在小钩上挂一质量为M的物块C并由静止释放,可使物块A对挡板P的压力恰为零,但不会离开P,求物块C下降的最大距离;
(2)若C的质量改为2M,则当A刚离开挡板P时,B的速度多大?

如图甲所示,力传感器A与计算机相连接,可获得力随时间变化的规律。 将力传感器固定在光滑水平桌面上,测力端通过轻质细绳与一滑块相连,调节传感器高度使细绳水平,滑块放在较长的小车上,滑块的质量m=1.0kg,小车的质量为M=0.65kg。一根轻质细绳跨过光滑的定滑轮,其一端连接小车,另一端系一只空沙桶,调节滑轮可使桌面上部细绳水平,整个装置先处于静止状态。现打开传感器的同时缓慢向沙桶里倒入沙子,当小车刚好开始运动时,立即停止倒沙子。若力传感器采集的F-t图象如乙图所示,请结合该图象,求:(重力加速度g=10m/s2)
(1)小车刚开始运动时沙桶及所装沙子的总质量m0和滑块与小车间的动摩擦因数μ;
(2)小车运动稳定后的加速度大小。
如图17所示,光滑绝缘水平桌面上固定一绝缘挡板P,质量分别为mA和mB的小物块A和B(可视为质点)分别带有+QA和+QB的电荷量,两物块由绝缘的轻弹簧相连,一不可伸长的轻绳跨过定滑轮,一端与物块B连接,另一端连接轻质小钩。整个装置处于正交的场强大小为E、方向水平向左的匀强电场和磁感应强度大小为B、方向水平向里的匀强磁场中。物块A,B开始时均静止,已知弹簧的劲度系数为K,不计一切摩擦及AB间的库仑力,在运动过程中物块A、B所带的电荷量不变,物块B不会碰到滑轮,物块A、B均不离开水平桌面。若在小钩上挂一质量为M的物块C并由静止释放,可恰使物块A对挡板P的压力为零,但不会离开P,则

(1)求物块C下落的最大距离;
(2)求小物块C下落到最低点的过程中,小物块B的电势能的变化量、弹簧的弹性势能变化量;
(3)若C的质量改为2M,求小物块A刚离开挡板P时小物块B的速度大小以及此时小物块B对水平桌面的压力。
如图甲所示,力传感器A与计算机相连接,可获得力随时间变化的规律。 将力传感器固定在光滑水平桌面上,测力端通过轻质细绳与一滑块相连,调节传感器高度使细绳水平,滑块放在较长的小车上,滑块的质量m=1.0kg,小车的质量为M=0.65kg。一根轻质细绳跨过光滑的定滑轮,其一端连接小车,另一端系一只空沙桶,调节滑轮可使桌面上部细绳水平,整个装置先处于静止状态。现打开传感器的同时缓慢向沙桶里倒入沙子,当小车刚好开始运动时,立即停止倒沙子。若力传感器采集的F-t图象如乙图所示,请结合该图象,求:(重力加速度g=10m/s2)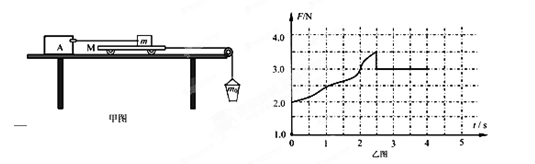
(1)小车刚开始运动时沙桶及所装沙子的总质量m0和滑块与小车间的动摩擦因数μ;
(2)小车运动稳定后的加速度大小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com