
题目列表(包括答案和解析)
如图8-3-24所示,在xOy平面内有足够大的匀强电场,电场方向竖直向上,电场强度E=40 N/C,在y轴左侧平面内有足够大的瞬时磁场,磁感应强度B1随时间t变化的规律如图乙所示,15π s后磁场消失,选定磁场垂直纸面向里为正方向.在y轴右侧平面内还有方向垂直纸面向外的恒定的匀强磁场,分布在一个半径为r=0.3 m的圆形区域(图中未画出),且圆的左侧与y轴相切,磁感应强度B2=0.8 T.t=0时刻,一质量m=8×10-4 kg\,电荷量q=2×10-4 C的微粒从x轴上xP=-0.8 m处的P点以速度v=0.12 m/s向x轴正方向入射.(g取10 m/s2,计算结果保留两位有效数字)


甲 乙
图8-3-24
(1)求微粒在第二象限运动过程中离y轴\,x轴的最大距离.
(2)若微粒穿过y轴右侧圆形磁场时,速度方向的偏转角度最大,求此圆形磁场的圆心坐标(x,y).
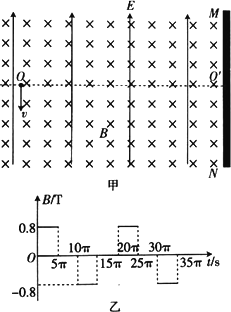
如图甲所示,竖直挡板MN的左侧空间有方向竖直向上的匀强电场和垂直纸面向里的水平匀强磁场,电场和磁场的范围足够大,电场强度的大小E=40N/C,磁感应强度的大小B随时间t变化的关系图象如图乙所示,选定磁场垂直纸面向里为正方向,在t=0时刻,一质量m=8×10-4 kg,带电荷q=+2×10-4C的微粒在O点具有竖直向下的速度v=0.12 m/s,![]() 是挡板MN上一点,直线
是挡板MN上一点,直线![]() 与挡板MN垂直,取g=10 m/s2.求:
与挡板MN垂直,取g=10 m/s2.求:
(1)微粒下一次经过直线![]() 时到O点的距离.
时到O点的距离.
(2)微粒在运动过程中离开直线![]() 的最大距离.
的最大距离.
(3)水平移动挡板,使微粒能垂直射到挡板上,挡板与O点间距离应满足的条件.
(2013·天津耀华中学一模,12题)(20分)如图甲,在圆柱形区域内存在一方向竖直向下,磁感应强度大小为B的匀强磁场,在此区域内,沿水平面固定一半径为r的圆环形光滑细玻璃管,环心O在区域中心。一质量为m,带电量为q(q>0)的小球,在管内沿逆时针方向(从上向下看)做圆周运动。已知磁感应强度大小B随时间t的变化关系如图乙所示,其中![]() ,设小球在运动过程中电量保持不变,对原磁场的影响可忽略。
,设小球在运动过程中电量保持不变,对原磁场的影响可忽略。
(1)在t=0到t=![]() :这段时间内,小球不受细管侧璧的作用力,求小球的速度大小
:这段时间内,小球不受细管侧璧的作用力,求小球的速度大小![]() ;
;
(2)在竖直向下的磁感应强度增大过程中;将产生涡旋电场,其电场线是在水平面内—系列沿逆时针方向的同心圆。同一条电场线上各点的场强大小相等,涡旋电场场强与电势差的关系与匀强电场相同。试求t=![]() 到t=l.5
到t=l.5![]() 这段时间内;
这段时间内;
① 细管内涡旋电场的场强大小E;
② 电场力对小球做的功W。

..(15分)如图甲所示,一固定的矩形导体线圈水平放置,线圈的两端接一只小灯泡,在线圈所在空间内存在着与线圈平面垂直的均匀分布的磁场.已知线圈的匝数n=100匝,电阻r=1.0 Ω,所围成矩形的面积S=0.040 m2,小灯泡的电阻R=9.0 Ω,磁场的磁感应强度按如图12乙所示的规律变化,线圈中产生的感应电动势的瞬时值表达式为e=nBmScos(t),其中Bm为磁感应强度的最大值,T为磁场变化的周期.不计灯丝电阻随温度的变化,求:
(1)线圈中产生的感应电动势的最大值;
(2)小灯泡消耗的电功率;
(3)在磁感应强度变化的0~的时间内,通过小灯泡的电荷量.
..(15分)如图甲所示,一固定的矩形导体线圈水平放置,线圈的两端接一只小灯泡,在线圈所在空间内存在着与线圈平面垂直的均匀分布的磁场.已知线圈的匝数n=100匝,电阻r=1.0 Ω,所围成矩形的面积S=0.040 m2,小灯泡的电阻R=9.0 Ω,磁场的磁感应强度按如图12乙所示的规律变化,线圈中产生的感应电动势的瞬时值表达式为e=nBmScos(t),其中Bm为磁感应强度的最大值,T为磁场变化的周期.不计灯丝电阻随温度的变化,求:
(1)线圈中产生的感应电动势的最大值;
(2)小灯泡消耗的电功率;
(3)在磁感应强度变化的0~的时间内,通过小灯泡的电荷量.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com