
题目列表(包括答案和解析)
如图所示,一个重为G的匀质球放在光滑斜面上,斜面倾角为α,在斜面上有一个光滑的不计厚度的木板挡住球,使之处于静止状态,今使板与斜面的夹角β缓慢增大,问:在此过程中,球对挡板和球对斜面的压力大小如何变化?

图4-2-28
【解析】:取球为研究对象,球受重力G、斜面支持力F1、挡板支持力F2,因为球始终处于平衡状态,故三个力的合力始终为零,三个力构成封闭的三角形,当挡板逆时针转动时,F2的方向也逆时针转动,作出如图所示的动态矢量三角形.由图可见,F2先减小后增大,F1随β增大而始终减小.

由牛顿第三定律知,球对挡板的压力先减小后增大,对斜面的压力始终减小.
如图所示,一个重为G的匀质球放在光滑斜面上,斜面倾角为α,在斜面上有一个光滑的不计厚度的木板挡住球,使之处于静止状态,今使板与斜面的夹角β缓慢增大,问:在此过程中,球对挡板和球对斜面的压力大小如何变化?
图4-2-28
【解析】:取球为研究对象,球受重力G、斜面支持力F1、挡板支持力F2,因为球始终处于平衡状态,故三个力的合力始终为零,三个力构成封闭的三角形,当挡板逆时针转动时,F2的方向也逆时针转动,作出如图所示的动态矢量三角形.由图可见,F2先减小后增大,F1随β增大而始终减小.
由牛顿第三定律知,球对挡板的压力先减小后增大,对斜面的压力始终减小.
如图所示,绳与杆均不计重力,承受力的最大值一定.A端用绞链固定,滑轮O在A点正上方(滑轮大小及摩擦均可忽略),杆B端吊一重物P,现施加拉力F将B缓慢上拉(均未断),在杆达到竖直前( )
图4-2-25
A.绳子越来越容易断 B.绳子越来越不容易断
C.杆越来越容易断 D.杆越来越不容易断
【解析】:选B.以B点为研究对象,B点受三个力:绳沿BO方向的拉力F,重物P竖直向下的拉力G,AB杆沿AB方向的支持力N.这三个力平衡,所构成的力的矢量三角形与几何三角形OAB相似,得到==,由此可知,N不变,F随OB的减小而减小.
.如图所示,用绳OA、OB和OC吊着重物P处于静止状态,其中绳OA水平,绳OB与水平方向成θ角.现用水平向右的力F缓慢地将重物P拉起,用FA和FB分别表示绳OA和绳OB的张力,则( )
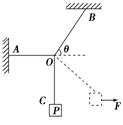
图4-9
A.FA、FB、F均增大
B.FA增大,FB不变,F增大
C.FA不变,FB减小,F增大
D.FA增大,FB减小,F减小
【解析】:选B.把OA、OB和OC三根绳和重物P看成一个整体,整体受到重力mg,A点的拉力FA,方向沿着OA绳水平向左,B点的拉力FB,方向沿着OB绳斜向右上方,水平向右的拉力F而处于平衡状态,有:FA=F+FBcosθ,FBsinθ=mg,因为θ不变,所以FB不变.再以O点进行研究,O点受到OA绳的拉力,方向不变,沿着OA绳水平向左,OB绳的拉力,大小和方向都不变,OC绳的拉力,大小和方向都可以变化,O点处于平衡状态,因此这三个力构成一个封闭的矢量三角形(如图),刚开始FC由竖直方向逆时针旋转到图中的虚线位置,因此FA和FC同时增大,又FA=F+FBcosθ,FB不变,所以F增大,所以B正确.
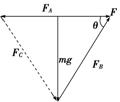
.如图所示,用绳OA、OB和OC吊着重物P处于静止状态,其中绳OA水平,绳OB与水平方向成θ角.现用水平向右的力F缓慢地将重物P拉起,用FA和FB分别表示绳OA和绳OB的张力,则( )
图4-9
A.FA、FB、F均增大
B.FA增大,FB不变,F增大
C.FA不变,FB减小,F增大
D.FA增大,FB减小,F减小
【解析】:选B.把OA、OB和OC三根绳和重物P看成一个整体,整体受到重力mg,A点的拉力FA,方向沿着OA绳水平向左,B点的拉力FB,方向沿着OB绳斜向右上方,水平向右的拉力F而处于平衡状态,有:FA=F+FBcosθ,FBsinθ=mg,因为θ不变,所以FB不变.再以O点进行研究,O点受到OA绳的拉力,方向不变,沿着OA绳水平向左,OB绳的拉力,大小和方向都不变,OC绳的拉力,大小和方向都可以变化,O点处于平衡状态,因此这三个力构成一个封闭的矢量三角形(如图),刚开始FC由竖直方向逆时针旋转到图中的虚线位置,因此FA和FC同时增大,又FA=F+FBcosθ,FB不变,所以F增大,所以B正确.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com