解析　(1)小球从曲面上滑下，只有重力做功，由机械能守恒定律知：

mgh＝mv                                                       ①

得v₀＝＝ m/s＝2 m/s.

(2)小球离开平台后做平抛运动，小球正好落在木板的末端，则

H＝gt²                                                                                                                                                      ②

＝v₁t                                                                                                                ③

联立②③两式得：v₁＝4 m/s

设释放小球的高度为h₁，则由mgh₁＝mv

得h₁＝＝0.8 m.

(3)由机械能守恒定律可得：mgh＝mv²

小球由离开平台后做平抛运动，可看做水平方向的匀速直线运动和竖直方向的自由落体运动，则：

y＝gt²                                                                                                                                                       ④

x＝vt                                                                                                                       ⑤

tan 37°＝                                                                                                          ⑥

v_y＝gt                                                                                                                      ⑦

v＝v²＋v                                                       ⑧

E_k＝mv                                                      ⑨

由④⑤⑥⑦⑧⑨式得：E_k＝32.5h                                                                       ⑩

考虑到当h>0.8 m时小球不会落到斜面上，其图象如图所示

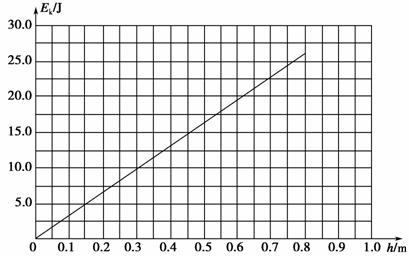
答案　(1)2 m/s　(2)0.8 m　(3)E_k＝32.5h　图象见解析

解析　(1)如图所示，画出通过P₁、P₂的入射光线，交AC面于O，画出通过P₃、P₄的出射光线交AB面于O′.则光线OO′就是入射光线P₁P₂在三棱镜中的折射光线．

(2)在所画的图上注明入射角θ₁和折射角θ₂，并画出虚线部分，用量角器量出θ₁和θ₂(或用直尺测出线段EF、OE、GH、OG的长度)．

(3)n＝；(或因为sin θ₁＝，sin θ₂＝，

则n＝＝)．

答案　见解析

 

解析　(1)整个装置沿斜面向上做匀速运动时，即整个系统处于平衡状态，

则研究A物体：f＝m_Agsin θ＝2 N，

研究整体：F＝(m_A＋m_B)gsin θ＋μ₂(m_A＋m_B)gcos θ＝21 N.

(2)整个装置沿斜面向上做匀加速运动，且A、B恰好没有相对滑动，则说明此时A、B之间恰好达到最大静摩擦力，

研究A物体：

f_max＝f_滑＝μ₁m_Agcos θ＝2.4 N，

f_max－m_Agsin θ＝m_Aa，

解得a＝1 m/s²，

研究整体：F－(m_A＋m_B)gsin θ－μ₂(m_A＋m_B)gcos θ＝(m_A＋m_B)a，

解得F＝23.4 N.

答案　(1)2 N　21 N　(2)2.4 N　23.4 N

解析　(1)设木板第一次上升过程中，物块的加速度为a_物块，由牛顿第二定律kmgsin θ－mgsin θ＝ma_物块

解得a_物块＝(k－1)gsin θ，方向沿斜面向上

(2)设以地面为零势能面，木板第一次与挡板碰撞时的速度大小为v₁

由机械能守恒得：×2mv＝2mgH

解得v₁＝

设木板弹起后的加速度为a_板，由牛顿第二定律得：

a_板＝－(k＋1)gsin θ

木板第一次弹起的最大路程s₁＝＝

木板运动的路程s＝＋2s₁＝

(3)设物块相对木板滑动距离为L

根据能量守恒mgH＋mg(H＋Lsin θ)＝kmgLsin θ

摩擦力对木板及物块做的总功W＝－kmgLsin θ

解得W＝－

答案　(1)(k－1)gsin θ；方向沿斜面向上

(2)　(3)－

如图所示，半径为R、圆心为O的大圆环固定在竖直平面内，两个轻质小圆环套在大圆环上．一根轻质长绳穿过两个小圆环，它的两端都系上质量为m的重物．忽略小圆环的大小．

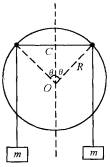
　　(1)将两个小圆环固定在大圆环竖直对称轴的两侧=30°的位置上(如图所示)．在两个小圆环间绳子的中点C处，挂上一个质量M=m的重物，使两个小圆环间的绳子水平，然后无初速释放重物M．设绳子与大、小圆环间的摩擦均可忽略，求重物M下降的最大距离．

　　(2)若不挂重物M，小圆环可以在大圆环上自由移动，且绳子与大、小圆环间及大、小圆环之间的摩擦均可以忽略，问两个小圆环分别在哪些位置时，系统可处于平衡状态？