
题目列表(包括答案和解析)
(10分)如图所示,固定于水平面上的金属架CDEF处在竖直向下的匀强磁场中,金属棒MN沿框架以速度v向右做匀速运动.t=0时,磁感应强度为B0,此时MN到达的位置使MDEN构成一个边长为l的正方形.为使MN棒中不产生感应电流,从t=0开始,磁感应强度B应怎样随时间t变化?请推导出这种情况下B与t的关系式.


 如图甲所示,两根足够长的平行导轨处在与水平方向成θ角的斜面上,θ=370,导轨电阻不计,间距L=0.3m.在斜面上加有磁感应强度B=1T、方向垂直于导轨平面向上的匀强磁场.导轨底端接一个阻值R=1Ω的电阻.质量m=1kg、电阻r=2Ω的金属棒ab横跨在平行导轨间,棒与导轨间的动摩擦因数μ=0.5,金属棒从距底端高为h1=2.0m处以平行于导轨向上的初速度v0=10m/s上滑,滑至最高点时高度为h2=3.2m,sin37°=0.6,cos37°=0.8,取g=10m/s2.
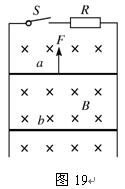
如图甲所示,两根足够长的平行导轨处在与水平方向成θ角的斜面上,θ=370,导轨电阻不计,间距L=0.3m.在斜面上加有磁感应强度B=1T、方向垂直于导轨平面向上的匀强磁场.导轨底端接一个阻值R=1Ω的电阻.质量m=1kg、电阻r=2Ω的金属棒ab横跨在平行导轨间,棒与导轨间的动摩擦因数μ=0.5,金属棒从距底端高为h1=2.0m处以平行于导轨向上的初速度v0=10m/s上滑,滑至最高点时高度为h2=3.2m,sin37°=0.6,cos37°=0.8,取g=10m/s2.如图19所示,在磁感应强度为B的水平方向的匀强磁场中竖直放置两平行导轨,磁场方向与导轨所在平面垂直。导轨上端跨接一阻值为R的电阻(导轨电阻不计)。两金属棒a和b的电阻均为R,质量分别为ma=2×10-2Kg和mb=1×10-2Kg,它们与导轨相连,并可沿导轨无摩擦滑动。闭合开关S,先固定b,用一恒力F向上拉a,稳定后a以v1=10m/s的速度匀速运动,此时再释放b,b恰好能保持静止,设导轨足够长,取g=10m/s2。
(1)求拉力F的大小;
(2)若将金属棒a固定,让金属棒b自由下滑(开关仍闭合),求b滑行的最大速度v2;
(3)若断开开关,将金属棒a和b都固定,使磁感应强度大小从B随时间均匀增加,经0.1s后磁感应强度增到2B时,a棒受到的安培力正好等于a棒的重力,求两金属棒间的距离h。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com