练习册

  • 练习册
  • 试题
    10．如图8所示.摆球的质量为m.从偏离水平方向θ＝30°的位置由静止释放.求: (1)小球运动到最低点A时绳子受到的拉力是多大? (2)整个过程中小球的机械能还守恒吗? 解析:(1)设悬线长为l.小球被释放后.先做自由落体运动.直到下落高度为h＝2lsinθ＝l.处于松弛状态的细绳被拉直为止．如图9所示.这时.小球的速度方向竖直向下.大小为v＝. 图9 当绳刚被拉直时.在绳的冲力作用下.速度v的法向分量vn减为零(相应的动能转化为绳的内能),小球以切向分量vτ＝vcos30°.开始做变速圆周运动到最低点．根据后一过程中机械能守恒.有 m(vcos30°)2+mgl＝mvA2 在最低点A.根据牛顿第二定律.又有F-mg＝m 所以.绳的拉力为F＝mg+m＝3.5mg. (2)整个过程中小球的机械能不守恒.细绳被拉直的瞬间小球的动能有损失.相应的动能转化为绳的内能． 答案:不守恒 图10 【查看更多】

     

    题目列表(包括答案和解析)

    质量为m、带电荷量为+q的小球用一绝缘细线悬于O点，开始时它在AB之间来回摆动，OA、OB与竖直方向OC的夹角均为θ，如图8-4-8所示.

    图8-4-8

    （1）如果当它摆动到B点时突然施加一竖直向上的、大小为E=mg/q的匀强电场，则此时线中的拉力T1=____________.

    （2）如果这一电场是在小球从A点摆到最低点C时突然加上去的，则当小球运动到B点时线中的拉力T2=____________.

    查看答案和解析>>

    利用如图8所示方法测定细线的抗拉强度.在长为L的细线下端悬挂一个很小的质量不计的盒子，小盒左侧开一孔，一个金属小球从斜轨道上释放后，水平进入小盒内，与小盒一起向右摆动.现逐渐提高金属小球在轨道上释放的高度，直至摆动时细线恰好被拉断，并测得此时金属小球平抛运动的竖直位移h和水平位移s，已知小球质量为m，该处重力加速度为g，试求该细线的抗拉断张力T多大？

    图8

    查看答案和解析>>

    如图所示，长为L=1.00m的非弹性轻绳一端系于固定点O，另一端系一质量为m=1.00kg的小球，将小球从O点正下方d=0.40m处，以水平初速度v0向右抛出，经一定时间绳被拉直．已知绳刚被拉直时，绳与竖直方向成53°角，sin53°=0.8，cos53°=0.6，重力加速度g取10m/s2．求：
    （1）小球水平抛出的初速度v0的大小．
    （2）小球摆到最低点时绳对小球的拉力大小．

    查看答案和解析>>

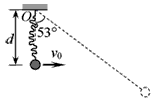
    如图所示，长为L=1.00m的非弹性轻绳一端系于固定点O，另一端系一质量为m=1.00kg的小球，将小球从O点正下方d=0.40m处，以水平初速度v0向右抛出，经一定时间绳被拉直。已知绳刚被拉直时，绳与竖直方向成53°角，sin53°=0.8，cos53°=0.6，重力加速度g取10m/s2。求：

    （1）小球水平抛出的初速度v0的大小。

    （2）小球摆到最低点时绳对小球的拉力大小。

    （3）小球能否到达最高点？若能求出小球到达最高点的速度；若不能，请写出判断的依据

    查看答案和解析>>

    如图所示，长为L=1.00m的非弹性轻绳一端系于固定点O，另一端系一质量为m=1.00kg的小球，将小球从O点正下方d=0.40m处，以水平初速度v0向右抛出，经一定时间绳被拉直。已知绳刚被拉直时，绳与竖直方向成53°角，sin53°=0.8，cos53°=0.6，重力加速度g取10m/s2。求：
    （1）小球水平抛出的初速度v0的大小。
    （2）小球摆到最低点时绳对小球的拉力大小。

    查看答案和解析>>


    同步练习册答案