某同学用如图1所示的装置测量弹簧的劲度系数k，当挂在弹簧下端的砝码处于静止状态时，测出弹簧受到的拉力F与对应的弹簧长度L（弹簧始终在弹性限度内），列表记录如下．

次数	F/N	L/cm
1	0.49	60.20
2	0.98	61.60
3	1.47	63.05
4	1.96	64.45
5	2.45	65.0

请在给定的坐标系中（如图2）作出F～L图线，并由图线计算出弹簧的劲度系数k=N/m．（结果保留二位有效数字）

实验题
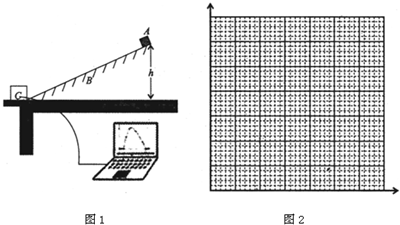
（1）如图1所示，质量为M的滑块A放在气垫导轨B上，C为速度传感器，它能将滑块A滑到导轨最低点时的速度实时传送到计算机上，整个装置置于高度可调节的斜面上，设斜面高度为h．启动气源，滑块4自导轨顶端由静止释放，将斜面的高度、滑块通过传感器C时的对应速度记人表中．（g取9.8m/s²）

实验序号	1	2	3	4	5	6
斜面高度h（cm）	10	20	30	40	50	60
传感器示数v（m/s）	1.40	1.98	2.42	2.80	2.90	3.43
v2（m2/s2）	1.96	3.92	5.86	7.84	8.41	11.76

①要由此装置验证机械能守恒定律，所需的器材有速度传感器（带电源、计算机、导线），滑块，气垫导轨（带气源），髙度可以调节的斜面，此外还需的器材有；
A、毫米刻度尺 　　　B、天平　　 C．秒表 　D．打点计时器 E弹簧测力计
②选择适当的物理量在如图2中所示的坐标纸上作出能直观反映滑块经传感器时的速度与斜面髙度的关系图象；（需标出横纵坐标所代表的物理量）
③由图象分析滑块沿气垫导轨下滑时机械能是否守恒．若守恒，说明机械能守恒的依据，若不守恒，说明机械能不守恒的原因．你的结论是；
（2）测一个待测电阻Rx（约200Ω）的阻值，除待测电阻外，实验室提供了如下器材：
电源E：电动势3V，内阻不计；
电流表A₁ 量程0～10mA、内阻r₁约为50Ω；
电流表A₂：量程0～50μA、内阻r₂=1000Ω；
滑动变阻器R₁：最大阻值20Ω、额定电流2A；
电阻箱R₂：阻值范围0～9999Ω
①由于没有提供电压表，为了测定待测电阻上的电压，应选电流表与电阻箱R₂连接，将其改装成电压表．
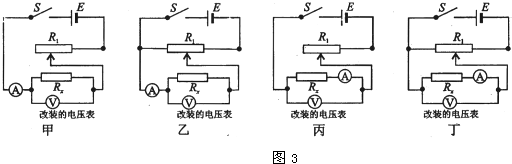
②对于下列测量R_x的四种电路图（如图3），为了测量准确且方便应选图．

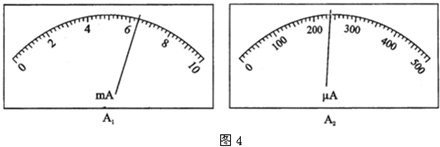
③实验中将电阻箱R₂的阻值调到4000Ω，再调节滑动变阻器R₁，两表的示数如图4所示，可测得待测电阻R_x的测量值是Ω

某同学用如图1所示装置“研究物体的加速度与外力关系”，他将光电门固定在气垫轨道上的某点B处，调节气垫导轨水平后，用重力为F的钩码，经绕过滑轮的细线拉滑块，每次滑块从同一位置A由静止释放，测出遮光条通过光电门的时间t．改变钩码个数，重复上述实验．记录的数据及相关计算如下表．

实验次数	1	2	3	4	5
F/N	0.49	0.98	1.47	1.96	2.45
t/（ms）	40.4	28.6	23.3	20.2	18.1
t2/（ms）2	1632.2	818.0	542.9	408.0	327.6
1 t2 /[×10-4(ms)-2]	6.1	12.2	18.4	24.5	30.6

（1）为便于分析F与t的关系，应作出F-

1

t2

的关系图象，请在坐标纸上（图2）作出该图线
（2）由图线得出的实验结论是：
（3）设AB间的距离为s，遮光条的宽度为d，请你由上述实验结论推导出物体的加速度a与时间t的关系式为

下面是某位同学进行研究性学习时的实验情况及记录．（如图1）其中L₀=3.5cm是弹簧的自由长．他记录了弹簧下端分别挂一个钩码、两个钩码、三个钩码和四个钩码时弹簧产生的弹力及相对应的弹簧长度，由此还得到了四次弹簧的伸长量．
（1）由表中的数据分析可知，弹簧产生的弹力与弹簧的（填“原长、后来的长、或形变量“）成正比．
      弹簧原长L₀=3.5cm

试验次数	1	2	3	4
钩码个数	1	2	3	4
弹簧弹力 F（N）	0.98	1.96	2.94	3.92
弹簧长度 L（cm）	4.0	4.5	5.0	5.5
弹簧伸长量 x（cm）	0.5	1.0	1.5	2.0

（2）请根据这位同学的数据记录，在F-x坐标纸上；
（3）根据图2中图象写出F与x之间的函数关系式，并说明式中各物理量及常数的单位；
（4）当弹簧下端挂500g的钩码时，弹簧的长度是cm．

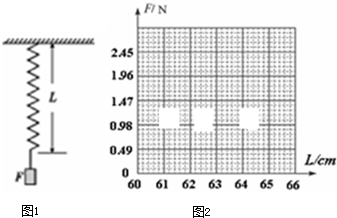
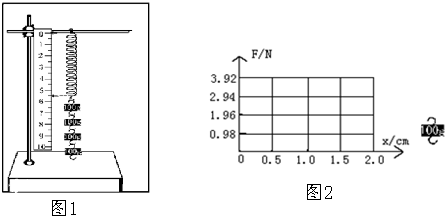
某实验小组用如图所示的装置测量弹簧的劲度系数k．当挂在弹簧下端的砝码处于静止状态时，测出弹簧受到的拉力F与对应的弹簧长度L（弹簧始终在弹性限度内），列表记录如下：

实验次数i	Fi（N）	Li（cm）
1	0.49	60.20
2	0.98	61.60
3	1.47	63.05
4	1.96	64.65
5	2.45	66.10
6	2.94	67.55

因为逐差法常用于处理自变量等间距变化的数据组，所以小组一成员用逐差法处理数据，具体如下：将表中第三列相邻的两项求差，得出弹簧伸长量△L=L_i-L_i-1，每个△L都是与相同的拉力△F=0.49N相对应的伸长量，求出△L的平均值

.

△L

=

(L2-L2)+(L 3-L 2)+…(L 6-L5)

5

=

L 6-L 1

5

=

67.55-60.20

5

cm=1.47cm
故该弹簧的劲度系数为k=

△F

. △L

=

0.49N

1.47cm

=0.333N/cm
该成员在实验数据处理中存在的问题是：；
请你用逐差法处理表格中的数据，尽量精确计算出弹簧的劲度系数k=N/cm（结果保留三位有效数字）．