
题目列表(包括答案和解析)
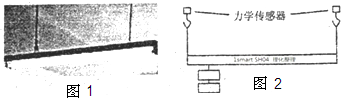
| 实验序号 | 拉力F作用点据左侧细线悬挂点距离△s | 木杆受到向下的拉力F(牛) | 左侧细线受到木杆对它的拉力F1(牛) | 右侧细线受到木杆对它的拉力F2(牛) |
| 1 | 0.3 | 10.0 | 7.0 | 3.0 |
| 2 | 0.3 | 20.0 | 14.0 | 6.0 |
| 3 | 0.3 | 30.0 | 21.0 | 9.0 |
| 4 | 0.4 | 10.0 | 6.0 | 4.0 |
| 5 | 0.4 | 20.0 | 12.0 | 8.0 |
| 6 | 0.4 | 30.0 | 18.0 | 12.0 |
| 7 | 0.5 | 10.0 | 5.0 | 5.0 |
| 8 | 0.5 | 20.0 | 10.0 | 10.0 |
| 9 | 0.5 | 30.0 | 15.0 | 15.0 |
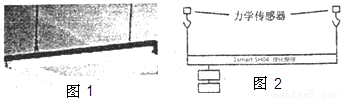
| 实验序号 | 拉力F作用点据左侧细线悬挂点距离△s | 木杆受到向下的拉力F(牛) | 左侧细线受到木杆对它的拉力F1(牛) | 右侧细线受到木杆对它的拉力F2(牛) |
| 1 | 0.3 | 10.0 | 7.0 | 3.0 |
| 2 | 0.3 | 20.0 | 14.0 | 6.0 |
| 3 | 0.3 | 30.0 | 21.0 | 9.0 |
| 4 | 0.4 | 10.0 | 6.0 | 4.0 |
| 5 | 0.4 | 20.0 | 12.0 | 8.0 |
| 6 | 0.4 | 30.0 | 18.0 | 12.0 |
| 7 | 0.5 | 10.0 | 5.0 | 5.0 |
| 8 | 0.5 | 20.0 | 10.0 | 10.0 |
| 9 | 0.5 | 30.0 | 15.0 | 15.0 |
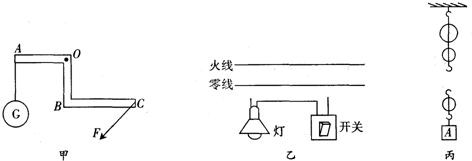
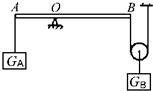 如图所示装置,杆的两端A、B离支点O的距离之比OA:OB=1:2.A端接一重为GA的物体,B端连一滑轮,滑轮上挂有另一重为GB的物体.现杠杆保持平衡,若不计滑轮重力,则GA与GB之比应是( )
如图所示装置,杆的两端A、B离支点O的距离之比OA:OB=1:2.A端接一重为GA的物体,B端连一滑轮,滑轮上挂有另一重为GB的物体.现杠杆保持平衡,若不计滑轮重力,则GA与GB之比应是( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com