
题目列表(包括答案和解析)
2012年10月15日,奥地利著名极限运动员鲍姆加特纳乘坐热气球从距地面高度约39km的高空跳下,并成功着陆.如图所示.该热气球由太空舱,绳索和气囊三部分组成.气囊与太空舱之间利用绳索连接.在加热过程中气囊中气体受热膨胀.密度变小,一部分气体逸出,当热气球总重力小于浮力时便开始上升.
假定鲍姆加特纳是在竖直方向上运动的,并经历了以下几个运动阶段:他首先乘坐热气球从地面开始加速上升到离地高h1=1km处,此阶段绳索对太空舱向上的总拉力恒为F1=3002.5N;接着再匀速上升到离地面高h2=38km处,此阶段绳索对太空舱向上的总拉力恒为F2=3000N;然后再减速上升到离地高h3=39km处,此阶段绳索对太空舱向上的总拉力恒为F3=2997.5N;他在上升过程中共用时t1=1×104s,在离地高39km处立即跳下.自由下落t2=4min后速度已超过音速,最后打开降落伞,又用时t3=16min又安全到达地面.忽略髙度对g的影响,取g=10N/kg.求:
①从离开地面到安全返回地面的整个过程中,运动员的平均速度是多少?(结果取整数)
②在热气球上升过程中.绳索对太空舱向上的总拉力做功的平均功率是多少?
③当热气球上升到离地高20km处.若热气球总质量(含气囊里面气体)m=7.18×104kg,整个热气球的体积V=8×105m3,整个热气球受到的空气阻力f=2×103N,不考虑气流(或风) 对热气球的影响.则此高度处的空气密度是多少?

如图1-11所示,在某学校举行的田径运动会上,质量为60 kg、身高为1.7 m的某运动员参加跳高比赛时的示意图.跳高前先将软绳的一端系在该运动员的腰部(重心处) ,另一端穿过固定在地面上的小环,然后,将绳子拉直后让运动员尽力往上跳.刚起跳时,该运动员的重心离地面的高度为身高的0.6倍,当运动员跳到最高点时,拉直的绳子从小环到该运动员腰部的总长度为1.8 m.(g=10 N/kg)则:
(1)在这个过程中,运动员重心上升的高度是多少?运动员跳高所做的功是多少?
(2)月球表面的引力是地球表面引力的1/6,如果该运动员按同样的方式起跳,那么,他在月球上能跳起的高度为多少?

图1-11
 物理学告诉我们,对每个星球来讲,下列公式成立:GM=gR2,这一关系式被称为“黄金变换”.其中:R是星球的半径,g为星球的表面重力常数,M为星球的质量,G为万有引力常量,G=6.67×10-11N?m2/kg2.
物理学告诉我们,对每个星球来讲,下列公式成立:GM=gR2,这一关系式被称为“黄金变换”.其中:R是星球的半径,g为星球的表面重力常数,M为星球的质量,G为万有引力常量,G=6.67×10-11N?m2/kg2.| v | 2 0 |
| ||
| g |
| v0 |
| g |
 物理学告诉我们,对每个星球来讲,下列公式成立:GM=gR2,这一关系式被称为“黄金变换”.其中:R是星球的半径,g为星球的表面重力常数,M为星球的质量,G为万有引力常量,G=6.67×10-11N?m2/kg2.
物理学告诉我们,对每个星球来讲,下列公式成立:GM=gR2,这一关系式被称为“黄金变换”.其中:R是星球的半径,g为星球的表面重力常数,M为星球的质量,G为万有引力常量,G=6.67×10-11N?m2/kg2.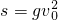 B.
B.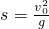 C.
C.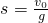 D.s=gv0
D.s=gv0湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com