
题目列表(包括答案和解析)
 过山车是游乐场中常见的设施,如图是一种过山车的简易模型.它由水平轨道和在竖直平面内的若干个光滑圆形轨道组成,A、B、C…分别是各个圆形轨道的最低点,第一圆轨道的半径R1=2.0m,以后各个圆轨道半径均是前一轨道半径的k倍(k=0.8),相邻两最低点间的距离为两点所在圆的半径之和.一个质量m=1.0kg的物块(视为质点),从第一圆轨道的左侧沿轨道向右运动,经过A点时的速度大小为v0=12m/s.已知水平轨道与物块间的动摩擦因数μ=0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求:
过山车是游乐场中常见的设施,如图是一种过山车的简易模型.它由水平轨道和在竖直平面内的若干个光滑圆形轨道组成,A、B、C…分别是各个圆形轨道的最低点,第一圆轨道的半径R1=2.0m,以后各个圆轨道半径均是前一轨道半径的k倍(k=0.8),相邻两最低点间的距离为两点所在圆的半径之和.一个质量m=1.0kg的物块(视为质点),从第一圆轨道的左侧沿轨道向右运动,经过A点时的速度大小为v0=12m/s.已知水平轨道与物块间的动摩擦因数μ=0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求: 过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=2.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点以v0=12m/s的初速度沿轨道向右运动,A、B间距L=11.5m.小滑块与水平轨道间的动摩擦因数μ=0.10.圆形轨道是光滑的,水平轨道足够长.取重力加速度g=10m/s2.求:
过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=2.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点以v0=12m/s的初速度沿轨道向右运动,A、B间距L=11.5m.小滑块与水平轨道间的动摩擦因数μ=0.10.圆形轨道是光滑的,水平轨道足够长.取重力加速度g=10m/s2.求: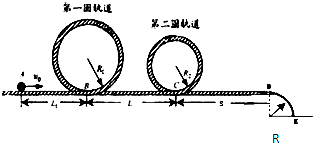 过山车是游乐场中常见的设施.某校物理兴趣小组自制过山车的简易模型,如图所示,它由水平轨道和在竖直平面内的圆形轨道组成,B、C分别是二个圆形轨道的最低点,半径分别是R1=2.0m、R2=1.4M,DE段是一半径为R3=1.0m的四分之一光滑圆弧轨道,它与水平轨道平滑连接,D点为圆弧的最高点,一个质量为M=1.0kg的小球(视为质点),从轨道的左侧A点以V0=12.0m/s的初速度沿轨道向右运动,A、B间距L1=6.0m.C、D间距S=15.0m,小球与水平轨道间的动摩擦因数μ=0.2,圆形轨道是光滑的.假设水平轨道足够长,圆形轨道间不相互重叠.重力加速度取g=10m/s2,试求:
过山车是游乐场中常见的设施.某校物理兴趣小组自制过山车的简易模型,如图所示,它由水平轨道和在竖直平面内的圆形轨道组成,B、C分别是二个圆形轨道的最低点,半径分别是R1=2.0m、R2=1.4M,DE段是一半径为R3=1.0m的四分之一光滑圆弧轨道,它与水平轨道平滑连接,D点为圆弧的最高点,一个质量为M=1.0kg的小球(视为质点),从轨道的左侧A点以V0=12.0m/s的初速度沿轨道向右运动,A、B间距L1=6.0m.C、D间距S=15.0m,小球与水平轨道间的动摩擦因数μ=0.2,圆形轨道是光滑的.假设水平轨道足够长,圆形轨道间不相互重叠.重力加速度取g=10m/s2,试求:(20分)![]() 过山车是游乐场中常见的设施。下图是一种过山车的简易模型,它由水平轨道和在竖直平面内的三个圆形轨道组成,B、C、D分别是三个圆形轨道的最低点,B、C间距与C、D间距相等,半径
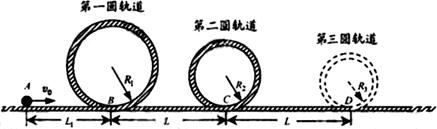
过山车是游乐场中常见的设施。下图是一种过山车的简易模型,它由水平轨道和在竖直平面内的三个圆形轨道组成,B、C、D分别是三个圆形轨道的最低点,B、C间距与C、D间距相等,半径![]() 、
、![]() 。一个质量为
。一个质量为![]() kg的小球(视为质点),从轨道的左侧A点以
kg的小球(视为质点),从轨道的左侧A点以![]() 的初速度沿轨道向右运动,A、B间距
的初速度沿轨道向右运动,A、B间距![]() m。小球与水平轨道间的动摩擦因数
m。小球与水平轨道间的动摩擦因数![]() ,圆形轨道是光滑的。假设水平轨道足够长,圆形轨道间不相互重叠。重力加速度取
,圆形轨道是光滑的。假设水平轨道足够长,圆形轨道间不相互重叠。重力加速度取![]() ,计算结果保留小数点后一位数字。试求
,计算结果保留小数点后一位数字。试求
(1)小球在经过第一个圆形轨道的最高点时,轨道对小球作用力的大小;
(2)如果小球恰能通过第二圆形轨道,B、C间距![]() 应是多少;
应是多少;
(3)在满足(2)的条件下,如果要使小球不能脱离轨道,在第三个圆形轨道的设计中,半径![]() 应满足的条件;小球最终停留点与起点
应满足的条件;小球最终停留点与起点![]() 的距离。
的距离。
![]()
(1)求它上升的最大高度及上升所用的时间;
(2)求返回最底端时的速度大小和返回最底端所用的时间.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com