
题目列表(包括答案和解析)
质量为m1的登月舱连接在质量为m2的轨道舱上一起绕月球作圆周运动,其轨道半径是月球半径Rm的3倍。某一时刻,登月舱与轨道舱分离,轨道舱仍在原轨轨道上运动,登月舱作一瞬间减速后,沿图示椭圆轨道登上月球表面,在月球表面逗留一段时间后,快速启动发动机,使登月舱具有一合适的初速度,使之沿原椭圆轨道回到脱离点与轨道舱实现对接。由开普勒第三定律可知,以太阳为焦点作椭圆轨道运行的所有行星,其椭圆轨道半长轴的立方与周期的平方之比是一个常量。另,设椭圆的半长轴为a,行星质量为m,太阳质量为M0,则行星的总能量为![]() 。行星在椭圆轨道上运行时,行星的机械能守恒,当它距太阳的距离为r时,它的引力势能为
。行星在椭圆轨道上运行时,行星的机械能守恒,当它距太阳的距离为r时,它的引力势能为![]() 。G为引力恒量。设月球质量为M,不计地球及其它天体对登月舱和轨道舱的作用力。求:
。G为引力恒量。设月球质量为M,不计地球及其它天体对登月舱和轨道舱的作用力。求:
(1)登月舱减速时,发动机做了多少功?
(2)登月舱在月球表面可逗留多长时间?

设探月卫星“嫦娥1号”绕朋运行的轨道是圆形的,且贴近月球表面。已知月球的质量M2约为地球质量M1的![]() ,月球的半径R2约为月球与地球距离R1的
,月球的半径R2约为月球与地球距离R1的![]() ,月球绕地球运动(看作圆周运动)的平均速率为v1=1.0km/s。“嫦娥1号”安装的太阳能电池帆板的面积S=8πm2。该太阳能电池将太阳能转化为电能的转化率η=11%。已知太阳光的总功率为P0=3.8×1026 W。月球与太阳之间的平均距离R=1.5×1011 m。估算(结果取2位有效数字)
,月球绕地球运动(看作圆周运动)的平均速率为v1=1.0km/s。“嫦娥1号”安装的太阳能电池帆板的面积S=8πm2。该太阳能电池将太阳能转化为电能的转化率η=11%。已知太阳光的总功率为P0=3.8×1026 W。月球与太阳之间的平均距离R=1.5×1011 m。估算(结果取2位有效数字)
(1)该探月卫星绕月运行的速率v2
(2)太阳光趋向太阳能电池帆板进太阳能电池的电功率P
“嫦娥一号”经过三次近月制动后环绕月球表面附近飞行,设地球、月球的质量分别分m1、m2,半径分别为R1、R2,人造地球卫星的第一宇宙速度为![]() 对应的环绕速度为T,则“嫦娥一号”环绕月球表面附近圆轨道飞行的速度和周期分别为
对应的环绕速度为T,则“嫦娥一号”环绕月球表面附近圆轨道飞行的速度和周期分别为
A.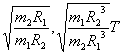 B.
B.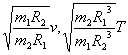
C.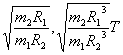 D.
D.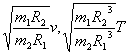

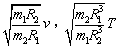
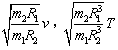
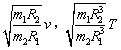
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com