
题目列表(包括答案和解析)
第一问 车和物体收到的力都是摩擦力
f=μmg 车的加速度a1=f/M=μmg/M=1m/s^2
滑块的加速度a2=f/m=μmg/m=5m/s^2
第二问 S=2.7m
假设不能从车上滑出 那么滑块最后必定停留在车上 并且和车具有同样的末速度 设为v'
因为系统在水平方向上所受的合外力为零 所以满足动量守恒
Mv+mv0=(M+m)*v' → v'=v0*m/(M+m)=7.5*10/(10+50)=1.25m/s
然后我们看能量 如果系统的初动能减去末动能 小于摩擦力所能做的最大功(就是滑块滑到头 但没掉下来) 那么假设成立 反之 不成立 不能明白的话 我们看下面具体的解答
先求系统的末动能 Ek'=1/2(M+m)v'^2=1/2*(50+10)*1.25^2=46.875(J)
系统的初动能 Ek=1/2mv0^2=1/2*10*7.5^2=281.25(J)
摩擦力所能做的最大功 W=fs=μmgs=0.5*10*10*3=150(J)
Ek-Ek'>W 所以也就是说 系统的初动能被摩擦力消耗掉一部分后【克服摩擦力做功】 所剩下的动能 还是要大于他们最后一起以同样的速度运动时的动能 因此滑块最后不肯能停在车上
那么 我们就来求滑块落地时与平板车右端间的水平距离
因为滑块滑出小车后 在水平方向上和小车都是做匀速运动
所以他们之间的距离 就是他们的速度差乘以滑块落地所需的时间
那么 我们就需要算出滑块的末速度v'和小车的末速度v''
现在有两个未知数 那就必须有两个方程
第一个方程是能量方程 Ek-W=1/2mv'^2+1/2Mv''^2
第二个方程是动量方程 mv0=mv'+Mv''
联立这两个方程 解得 v''=0.5m/s 或 v''=2m/s(舍掉)
从而得到v'=5m/s
接下来算滑块落地要多长时间
由h=1/2gt^2 带入数据 得t=0.6s
所以最后的答案: S=(v'-v'')*t=4.5*0.6=2.7m

| S2+S3 |
| 2T |
| S2+S3 |
| 2T |
| (S4+S5+S6)-(S1+S2+S3) |
| 9T2 |
| (S4+S5+S6)-(S1+S2+S3) |
| 9T2 |
| (S4+S5+S6)-(S1+S2+S3) |
| 9T2 |
| (S4+S5+S6)-(S1+S2+S3) |
| 9T2 |
| U1 |
| R1+R0 |
| U2 |
| R2+R0 |
| 1 |
| U |
| 1 |
| U |
| 1 |
| R+R0 |
| 1 |
| R+R0 |
要求摩托车由静止开始在尽量短的时间内走完一段直道,然后驶入一段半圆形的弯道,但在弯道上行驶时车速不能太快,以免因离心作用而偏出车道.求摩托车在直道上行驶所用的最短时间.有关数据见表格.
|
启动加速度a1 |
4 m/s2 |
|
制动加速度a2 |
8 m/s2 |
|
直道最大速度v1 |
40 m/s |
|
弯道最大速度v2 |
20 m/s |
|
直道长度s |
218 m |
某同学是这样解的:要使摩托车所用时间最短,应先由静止加速到最大速度v1=40 m/s,然后再减速到v2=20 m/s,t1=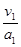 =…;t2=
=…;t2=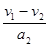 =…;t=t1+t2,你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请说明理由,并用你自己的方法算出正确结果.
=…;t=t1+t2,你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请说明理由,并用你自己的方法算出正确结果.
要求摩托车由静止开始在尽量短的时间内走完一段直道,然后驶入一段半圆形的弯道,但在弯道上行驶时车速不能太快,以免因离心作用而偏出车道。求摩托车在直道上行驶所用的最短时间.有关数据见表格。
| 启动加速度大小a1 | 4 m/s2 |
| 制动加速度大小a2 | 8 m/s2 |
| 直道最大速度v1 | 40 m/s |
| 弯道最大速度v2 | 20 m/s |
| 直道长度 s | 218 m |
注:制动加速度为匀减速时的加速度
某同学是这样解的:要使摩托车所用时间最短,应先由静止加速到最大速度v1=40 m/s,
然后再减速到v2=20 m/s,t1==…;t2=
=…;t=t1+t2?
你认为这位同学的解法是否合理?若合理,请完成计算;若不合理,请说明理由,并用你自己的方法算出正确结果。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com