练习册

  • 练习册
  • 试题
    2．绳索.弹簧以及杆是中学物理中常见的约束元件.它们的特性是不同的.现列表对照如下: [例9] 在车箱的顶板上用细线挂着一个小球(图1).在下列情况下可对车厢的运动情况得出怎样的判断: (1)细线竖直悬挂: ; (2)细线向图中左方偏斜: (3)细线向图中右方偏斜: . [分析]作用在小球上只能有两个力:地球对它的重力mg.细线对它的拉力T．根据这两个力是否处于力平衡状态.可判知小球所处的状态.从而可得出车厢的运动情况. (1)小球所受的重力mg与弹力T在一直线上.如图2(a)所示.且上.下方向不可能运动.所以小球处于力平衡状态.车厢静止或作匀速直线运动. (2)细线左偏时.小球所受重力mg与弹力T不在一直线上[如图2(b)].小球不可能处于力平衡状态．小球一定向着所受合力方向产生加速度．所以.车厢水平向右作加速运动或水平向左作减速运动． 同理.车厢水平向左作加速运动或水平向右作减速运动[图2(c)]． [说明] 力是使物体产生加速度的原因.不是产生速度的原因.因此.力的方向应与物体的加速度同向.不一定与物体的速度同向．如图2(b)中.火车的加速度必向右.但火车可能向左运动,图2(c) 中.火车的加速度必向左.但火车可能向右运动． [例10]如图1.人重600牛.平板重400牛.如果人要拉住木板.他必须用多大的力? [误解]对滑轮B受力分析有 2F=T 对木板受力分析如图2.则N+F=N+G板 又N=G人 [正确解答一]对滑轮B有 2F=T 对人有 N+F=G人 对木板受力分析有F+T=G板+N [正确解答二]对人和木板整体分析如图3.则 T+2F=G人+G板 由于T=2F [错因分析与解题指导][误解]错误地认为人对木板的压力等于人的重力.究其原因是没有对人进行认真受力分析造成的. [正确解答一.二]选取了不同的研究对象.解题过程表明.合理选取研究对象是形成正确解题思路的重要环节.如果研究对象选择不当.往往会使解题过程繁琐费时.并容易发生错误.通常在分析外力对系统的作用时.用整体法,在分析系统内物体间相互作用时.用隔离法.在解答一个问题需要多次选取研究对象时.可整体法和隔离法交替使用. [例11]如图1甲所示.劲度系数为k2的轻质弹簧.竖直放在桌面上.上面压一质量为m的物块.另一劲度系数为k1的轻质弹簧竖直地放在物块上面.其下端与物块上表面连接在一起.要想使物块在静止时.下面弹簧承受物重的2/3.应将上面弹簧的上端A竖直向上提高的距离是多少? [分析] 由于拉A时.上下两段弹簧都要发生形变.所以题目给出的物理情景比较复杂.解决这种题目最有效的办法是研究每根弹簧的初末状态并画出直观图.清楚认识变化过程 如图1乙中弹簧2的形变过程.设原长为x20.初态时它的形变量为△x2.末态时承重2mg/3.其形变量为△x2′.分析初末态物体应上升△x2-△x2′． 对图丙中弹簧1的形变过程.设原长为x10．受到拉力后要承担物重的1/3.则其形变是为△x1.则综合可知A点上升量为 d=△x1+△x2-△x2′ [解]末态时对物块受力分析如图2依物块的平衡条件和胡克定律 F1+F2′=mg (1) 初态时.弹簧2弹力 F2 = mg = k2△x2(2) 式可得 由几何关系 d=△x1+△x2-△x2′ (4) [说明] 从前面思路分析可知.复杂的物理过程.实质上是一些简单场景的有机结合．通过作图.把这个过程分解为各个小过程并明确各小过程对应状态.画过程变化图及状态图等.然后找出各状态或过程符合的规律.难题就可变成中档题.思维能力得到提高. 轻质弹簧这种理想模型.质量忽略不计.由于撤去外力的瞬时.不会立即恢复形变.所以在牛顿定律中.经常用到,并且由于弹簧变化时的状态连续性.在动量等知识中也经常用到.这在高考中屡见不鲜． [例12]如图1所示.在倾角α=60°的斜面上放一个质量m的物体.用k=100N/m的轻弹簧平行斜面吊着．发现物体放在PQ间任何位置恰好都处于静止状态.测得AP=22cm.AQ=8cm.则物体与斜面间的最大静摩擦力等于多少? 物体位于Q点时.弹簧必处于压缩状态.对物体的弹簧TQ沿斜面向下,物体位于P点时.弹簧已处于拉伸状态.对物体的弹力Tp沿斜面向上．P.Q两点是物体静止于斜面上的临界位置.此时斜面对物体的静摩擦力都达到最大值fm.其方向分别沿斜面向下和向上． [解] 作出物体在P.Q两位置时的受力图(图2).设弹簧原长为L0.则物体在Q和P两处的压缩量和伸长量分别为 x1=L0-AQ.x2=AP-L0． 根据胡克定律和物体沿斜面方向的力平衡条件可知: kx1 =k(L0-AQ)=fm - mgsinα. kx2 =k(AP-L0)=fm + mgsinα． 联立两式得 [说明] 题中最大静摩擦力就是根据物体的平衡条件确定的.所以画出P.Q两位置上物体的受力图是至关重要的． [例13]质量均为m的四块砖被夹在两竖直夹板之间.处于静止状态.如图1.试求砖3对砖2的摩擦力. [误解]隔离砖“2 .因有向下运动的趋势.两侧受摩擦力向上. [正确解答]先用整体法讨论四个砖块.受力如图2所示.由对称性可知.砖“1 和“4 受到的摩擦力相等.则f=2mg,再隔离砖“1 和“2 .受力如图3所示.不难得到f′=0. [错因分析与解题指导][误解]凭直觉认为“2 和“3 间有摩擦.这是解同类问题最易犯的错误.对多个物体组成的系统内的静摩擦力问题.整体法和隔离法的交替使用是解题的基本方法. 本题还可这样思考:假设砖“2 与“3 之间存在摩擦力.由对称性可知.f23和f32应大小相等.方向相同.这与牛顿第三定律相矛盾.故假设不成立.也就是说砖“2 与“3 之间不存在摩擦力. 利用对称性解题是有效.简便的方法.有时对称性也是题目的隐含条件.本题砖与砖.砖与板存在五个接触面.即存在五个未知的摩擦力.而对砖“1 至“4 只能列出四个平衡方程.如不考虑对称性.则无法求出这五个摩擦力的具体值. 【查看更多】

     

    题目列表(包括答案和解析)

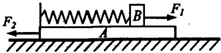    精英家教网如图所示，一劲度系数为k的轻弹簧左端固定在长且薄的木板A的左侧，轻弹簧右端与小物块B连接，已知木板A的质量为mA，小物块B的质量为mB．且A、B之间、以及A与水平地面间均光滑．开始时，A和B均静止，现同时对A、B施加等大反向的水平恒力F1和F2，即F1=F2=F．设整个过程中弹簧的形变不超过其弹性限度，B始终未滑离A．求：
    （1）以地面作为参照系，求当木板A的位移为lA时，物块B的位移lB的大小；
    （2）当弹簧的伸长量最大时，木板A的位移lA'是多大？并求这时由A、B及弹簧组成的系统所具有的机械能E．

    查看答案和解析>>

    （08衡水中学一调）（18分）如图所示，光滑水平面上有一质量M＝4.0kg的平板车，车的上表面右侧是一段长L＝1.0m的水平轨道，水平轨道左侧连一半径R=0.25m的1/4光滑圆弧轨道，圆弧轨道与水平轨道在O/点相切．车右端固定一个尺寸可以忽略、处于锁定状态的压缩弹簧，一质量m＝1.0kg的小物块紧靠弹簧，小物块与水平轨道间的动摩擦因数μ＝0.5．整个装置处于静止状态，现将弹簧解除锁定，小物块被弹出，恰能到达圆弧轨道的最高点A，g取10m/s2．求：

    （1）解除锁定前弹簧的弹性势能；

    （2）小物块第二次经过O/点时的速度大小；

    （3）最终小物块与车相对静止时距O/点的距离．

    查看答案和解析>>

    如图所示,一劲度系数为k的轻弹簧左端固定在长且薄的木板A的左端,轻弹簧右端与小物块B连接,已知木板A的质量为mA,小物块B的质量为mB,且A、B之间以及A与水平地面间均光滑.开始时,A和B均静止,现同时对A、B施加等大反向的水平恒力F1和F2,即F1=F2=F.设整个过程中弹簧的形变不超过其弹性限度,B始终未滑离A.求:

    (1)以地面作为参考系,求当木板A的位移为lA时,物块B的位移lB的大小;

    (2)当弹簧的伸长量最大时,木板A的位移lA′是多大?并求这时由A、B及弹簧组成的系统所具有的机械能E.

    查看答案和解析>>

        （08年石室中学模拟）如图所示，在足够大的光滑水平面上放有质量相等的物块A和B，其中A物块连接一个轻弹簧并处于静止状态，B物块以速度vo向着A物块运动。当物块与弹簧作用时，两物块在同一条直线上运动。则在A、B与弹簧相互作用地过程中，两物块A和B的v-t图象正确的是（    ）

     

       

    查看答案和解析>>

    如图所示，一劲度系数为k的轻弹簧左端固定在长且薄的木板A的左侧，轻弹簧右端与小物块B连接，已知木板A的质量为mA，小物块B的质量为mB．且A、B之间、以及A与水平地面间均光滑．开始时，A和B均静止，现同时对A、B施加等大反向的水平恒力F1和F2，即F1=F2=F．设整个过程中弹簧的形变不超过其弹性限度，B始终未滑离A．求：
    （1）以地面作为参照系，求当木板A的位移为lA时，物块B的位移lB的大小；
    （2）当弹簧的伸长量最大时，木板A的位移lA'是多大？并求这时由A、B及弹簧组成的系统所具有的机械能E．

    查看答案和解析>>


    同步练习册答案