
题目列表(包括答案和解析)
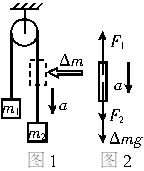
如图1所示,一轻绳跨过一固定的滑轮,两端各连接质量分别为m1和m2的物体.为不失一般性,设m1<m2.放手后m2将加速下降,m1加速上升,加速度大小均为a.注意此时轻绳也将做变速运动,为判断绳中张力大小是否处处相等,如图1中所示可以隔离质量为Δm的一小段绳子加以研究,其受力分析如图2所示,Δmg为绳子本身所受的重力,F1、F2分别为上、下绳子的拉力.由牛顿第二定律有Δmg+F2-F1=Δma.由于整段绳为轻绳即质量可以忽略不计,故Δm趋近于零,而加速度a为有限值,因此F2=F1,即不论轻绳是否平衡均满足张力大小处处相等.
力学问题的研究对象中有很多所谓的轻小物体,其特点之一就是可以忽略质量,同时也可以忽略重力.从上面的分析知可同样对其作受力分析,利用牛顿运动定律求解有关问题.
例2 如图3所示,一小球在纸面内来回摆动.当轻绳OA与OB拉力相等时,摆线OC与竖直面夹角θ为( )
A.15° B.30° C.45° D.60°
A.2个
B.3个
C.4个
D.5个

如图所示,质量为m的小物块(可以看成是质点)A放在粗糙的水平上,受到一个与水平面或θ角的斜向上的拉力F的作用,在水平面上运动。对A进行受力分析,则它受到的作用力的个数可能是[ ]
A.2个
B.3个
C.4个
D.5个

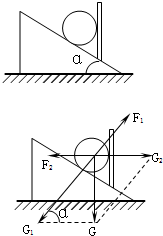 如图,小球质量为m,斜面倾角为α,档板竖直固定.求小球对档板和斜面的压力.有一位同学的解答如下:
如图,小球质量为m,斜面倾角为α,档板竖直固定.求小球对档板和斜面的压力.有一位同学的解答如下:如图所示,在绝缘水平面上放置一质量为m=2.0×10-3kg的带正电的小滑块A,所带电荷量为q=1.0×10-7C.在A的左边l=0.9m处放置一个质量为M=6.0×10-3kg的不带电的小滑块B,滑块B与左边竖直绝缘墙壁相距s=0.05m,滑块与水平面间的动摩擦因数为μ=0.50.在水平面上方空间加一方向水平向左的匀强电场,电场强度为E=4.0×105N/C.A由静止开始向左滑动并与B发生碰撞,设碰撞过程的时间极短,碰撞后两滑块结合在一起共同运动并与墙壁相碰撞,在与墙壁碰撞时没有机械能损失,也没有电荷量的损失,且两滑块始终没有分开,两滑块的体积大小可忽略不计.(g取10m/s2)

(1)试通过计算分析A与B相遇前A的受力情况和运动情况、A与B碰撞粘合后至A和B与墙壁碰撞前的受力情况和运动情况,以及A和B与墙壁碰撞后的受力情况和运动情况。
(2)两滑块在粗糙水平面上运动的整个过程中,由于摩擦而产生的热量是多少?(结果保留两位有效数字)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com