
题目列表(包括答案和解析)
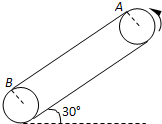 如图所示,皮带传动装置与水平面夹角为30°,轮半径R=
如图所示,皮带传动装置与水平面夹角为30°,轮半径R=| 1 |
| 2π |
| ||
| 6 |
| 252 |
| 396 |
| 1 |
| 2π |
| ||
| 6 |
| 252 |
| 396 |
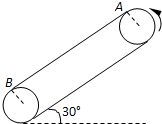
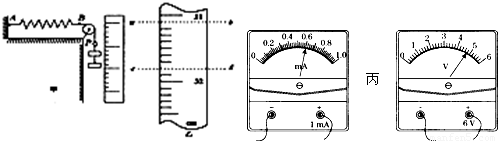
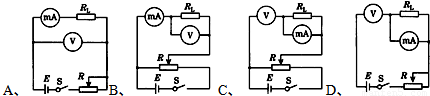
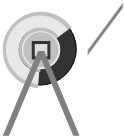 (2011?上海二模)某同学通过设计实验来探究物体因绕轴转动而具有的转动动能与哪些因素有关,他以圆型砂轮为研究对象,研究其转动动能与其质量、半径、角速度等的具体关系.如图所示,砂轮由动力带动匀速旋转,测得其角速度为ω,然后让砂轮脱离动力,用一把弹性尺子与砂轮接触使砂轮慢慢停下,设尺和砂轮间的摩擦力恒为
(2011?上海二模)某同学通过设计实验来探究物体因绕轴转动而具有的转动动能与哪些因素有关,他以圆型砂轮为研究对象,研究其转动动能与其质量、半径、角速度等的具体关系.如图所示,砂轮由动力带动匀速旋转,测得其角速度为ω,然后让砂轮脱离动力,用一把弹性尺子与砂轮接触使砂轮慢慢停下,设尺和砂轮间的摩擦力恒为| 10 |
| π |
| 半径/cm | 质量/m0 | 角速度/rad?s-1 | 圈数 | 转动动能/J |
| 4 | 1 | 2 | 8 | 6.4 |
| 4 | 1 | 3 | 18 | 14.4 |
| 4 | 1 | 4 | 32 | 25.6 |
| 4 | 2 | 2 | 16 | 12.8 |
| 4 | 3 | 2 | 24 | |
| 4 | 4 | 2 | 32 | 25.6 |
| 8 | 1 | 2 | 16 | 25.6 |
| 12 | 1 | 2 | 24 | |
| 16 | 1 | 2 | 32 | 102.4 |
(16分)探究能力是物理学研究的重要能力之一.有同学通过设计实验来探究物体因绕轴转动而具有的转动动能与哪些因素有关。他以圆型砂轮为研究对象,研究其转动动能与其质量、半径、角速度等的具体关系。如图16所示,砂轮由动力带动匀速旋转测得其角速度ω,然后让砂轮脱离动力,用一把弹性尺子与砂轮接触使砂轮慢慢停下,设尺和砂轮间的摩擦力恒为![]() ,(不计转轴的质量及其与支架间的摩擦)分别取不同质量、不同半径的砂轮,使其以不同角速度旋转的进行实验,最后得到的数据如下表所示:
,(不计转轴的质量及其与支架间的摩擦)分别取不同质量、不同半径的砂轮,使其以不同角速度旋转的进行实验,最后得到的数据如下表所示:
| 半径/cm | 质量/m0 | 角速度/rad·s-1 | 圈数 | 转动动能/J |
| 4 | 1 | 2 | 8 |
|
| 4 | 1 | 3 | 18 |
|
| 4 | 1 | 4 | 32 |
|
| 4 | 2 | 2 | 16 |
|
| 4 | 3 | 2 | 24 |
|
| 4 | 4 | 2 | 32 |
|
| 8 | 1 | 2 | 16 |
|
| 12 | 1 | 2 | 24 |
|
| 16 | 1 | 2 | 32 |
|
(1)根据题给数据计算砂轮的转动动能Ek,并填在上面的表格里。
(2)由上述数据推导出该砂轮的转动动能Ek与质量m、角速度ω、半径r的关系式为_____________。
(3)以上实验运用了物理学中的一个重要的思维方法是:_________________。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com