
题目列表(包括答案和解析)
某人造地球卫星的高度是地球半径的15倍。试估算此卫星的线速度。已知地球半径R=6400km,g=10m/s2。
某人造地球卫星绕地球做匀速圆周运动,设地球半径为R,地面的重力加速度为g正确的是
[ ]
A.人造地球卫星的最小周期为2π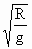
B.人造地球卫星的最小环绕速率为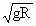
C.人造地球卫星在距地面高R处的绕行速度为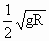
D.人造地球卫星在离地面高R处的加速度为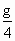
某人造地球卫星质量为m,其绕地球运动的轨道为椭圆.已知它在近地点时距离地面高度为h1,速率为v1,加速度为a1,在远地点时距离地面高度为h2,速率为v2,设地球半径为R,则该卫星.
(1)由近地点到远地点过程中地球对它的万有引力所做的功是多少?
(2)在远地点运动的加速度a2多大?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com