在“探究小车速度随时间变化规律”的实验中,某同学测量数据后,通过计算到了小车运动过程中各计时时刻的速度如表格所示:
| 位置编号 |
0 |
1 |
2 |
3 |
4 |
5 |
| 时间t/s |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
| 速度v/m?s-1 |
0.38 |
0.63 |
0.88 |
1.12 |
1.38 |
1.63 |
因此次实验的原始纸带没有保存,另一同学想估算小车从位置0到位置5的位移,其所用方法是将每个0.1s视为匀速运动,然后估算如下:
x=(0.38×0.1+0.63×0.1+0.88×0.1+1.12×0.1+1.38×0.1)那么,该同学得到的位移
小于
小于
.(选填“大于”、“等于”或“小于”)实际位移,为了使计算位移的误差尽可能小,你认为采取什么方法更合适,为什么?(不必算出具体数据)
可以先计算相邻位置间的平均速度,再得到位移,这是因为表中每隔0.1s的速度增加在误差范围内相同,即为匀变速直线运动,平均速度可以由公式
=求出,还可以求出加速度,应用匀变速直线运动公式
x=v0t+at2得出位移.
可以先计算相邻位置间的平均速度,再得到位移,这是因为表中每隔0.1s的速度增加在误差范围内相同,即为匀变速直线运动,平均速度可以由公式
=求出,还可以求出加速度,应用匀变速直线运动公式
x=v0t+at2得出位移.
.


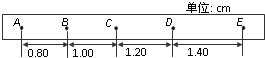 在“探究小车速度随时间变化规律”的实验中,打点计时器在纸带上依次打出一系列的点A,B,C,D,E,…,相邻两点间的距离如图所示,计时器打点周期为0.02s,则打c点时的瞬间,纸带的速度大小为
在“探究小车速度随时间变化规律”的实验中,打点计时器在纸带上依次打出一系列的点A,B,C,D,E,…,相邻两点间的距离如图所示,计时器打点周期为0.02s,则打c点时的瞬间,纸带的速度大小为