练习册

  • 练习册
  • 试题
    (二)机械能守恒定律的应用 ［例3］ 一个物体从光滑斜面顶端由静止开始滑下.斜面高1 m.长2 m.不计空气阻力.物体滑到斜面底端的速度是多大? 物体沿光滑斜面下滑时机械能守恒 分析:斜面是光滑的.不计摩擦.又不计空气阻力.物体所受的力有重力和斜面的支持力.支持力与物体的运动方向垂直.不做功.物体在下滑过程中只有重力做功.所以可用机械能守恒定律求解. 解析:题中没有给出物体的质量.可设物体的质量为m.物体在开始下滑到达斜面底端时的速度为v,则有Ep2=0, ,末状态的机械能.此时.Ep1=mgh.Ek1=0.初状态的机械能Ek1+Ep1=mgh. 根据机械能守恒定律有 Ek2+Ep2=Ek1+Ep1 . 所以. [方法引导] 这个问题也可以应用牛顿第二定律和运动学公式求解.但是应用机械能守恒定律求解.在思路和步骤上比较简单.在这个例题中.如果把斜面换成光滑的曲面.同样可以应用机械能守恒定律求解.要直接用牛顿第二定律求解.由于物体在斜面上所受的力是变力.处理起来就困难得多. 物体沿光滑曲面下滑时机械能守恒 ［例4］把一个小球用细绳悬挂起来.就成为一个摆.摆长为L.最大偏角为θ.小球运动到最低位置时的速度是多大? 分析:小球受两个力:重力和悬线的拉力.悬线的拉力始终垂直于小球的运动方向.不做功.小球在摆动过程中.只有重力做功.所以可用机械能守恒定律求解. 解析:选择小球在最低位置时所在的水平面为参考平面.小球在最高点时为初状态.初状态的动能Ek1＝0.重力势能Ep1=mg(L-Lcosθ).机械能Ek1+Ep1=mg(L-Lcosθ).小球在最低点时为末状态.末状态的动能,重力势能Ep2=0,末状态的机械能为. 根据机械能守恒定律有 Ek2+Ep2=Ek1+Ep1 所以. [教师精讲] 由这两个例题可以看出.应用机械能守恒定律解题.可以只考虑运动的初状态和末状态.不必考虑两个状态之间的过程的细节.这可以避免直接用牛顿第二定律解题的困难.简化解题的步骤. 守恒定律不仅给处理问题带来方便.而且有更深刻的意义.自然界千变万化.但有些物理量在一定条件下是守恒的.可以用这些“守恒量 表示自然界的变化规律.这就是守恒定律.寻求“守恒量 已经成为物理学研究中的重要方面.我们学习物理.要学会运用守恒定律处理问题. 【查看更多】

     

    题目列表(包括答案和解析)

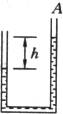
    (机械能守恒定律的应用)如图所示，U形管内装有同种液体，在管口右端用盖板A密封，两液面的高度差为h，U形管中液柱总长度为4h，U形管均匀且内壁光滑，现突然拿去盖板A，液体开始流动，求两液面相平时液体的速度大小．

    查看答案和解析>>

    （1）在“验证机械能守恒定律”的实验中，若应用公式v=gt计算即时速度进行验证，打点计时器所接交流电的频率为50Hz，甲、乙两条实验纸带如图所示，应选
    甲
    甲
    纸带好．

    （2）在“验证机械能守恒定律”的实验中，已知打点计时器所用电源的频率为50Hz，查得当地的重力加速度是9.80m/s2，测得所用重物的质量为1.00kg．如图所示，实验中得到一条点迹清晰的纸带，把第一个点记作O，另选连续的4个点A、B、C、D作为测量的点．经测量知道A、B、C、D各点到O点的距离分别为62.99cm、70.18cm、77.76cm、85.73cm，根据以上数据，可知重物由O点运动到C点重力势能的减少量等于
    7.62
    7.62
     J，动能的增加量等于
    7.56
    7.56
     J．（取三位有效数字）

    查看答案和解析>>

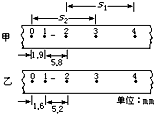    精英家教网在利用自由落体运动验证机械能守恒定律的实验中，
    （1）若应用公式v=gt计算即时速度进行验证，打点计时器所接交流电的频率为50赫兹，甲、乙两条实验纸带，如图所示，应选
     
    纸带好．
    （2）若通过测量纸带上某两点间距离来计算即时速度，进行验证，设已测得点2到4间距离为s1，点0到3间距离为s2，打点周期为T，为验证重物开始下落到打点计时器打下点3这段时间内机械能守恒、实验后，s1、s2和T应满足的关系为T=
     
    ．

    查看答案和解析>>

    在“验证机械能守恒定律”的实验中，下面叙述正确的是（　　）
    A、应用天平称出物体的质量B、应当选用点迹清晰，特别是第一个点没有拉成长条的纸带C、操作时应先放纸带后接电源D、打点计时器应接在电压为4～6V的交流电源上

    查看答案和解析>>

    （1）常用螺旋测微器的精度0.01mm，如图所示的螺旋测微器的读数为5.620mm，请你在刻度旁边的方框内标出符合该读数的数字．
    （2）在利用打点计时器做《验证机械能守恒定律的实验中》必须应用的测量仪器是
    B
    B
    （填序号）．
    A．游标卡尺     B．刻度尺       C．天平        D．秒表
    （3）给你下列器材：待测电压表（量程为3V，内阻RV约几千欧），电阻箱、滑动变阻器、6V蓄电池、电键、导线若干．试设计测定电压表内阻的实验原理图．

    查看答案和解析>>


    同步练习册答案