质量为m、电荷量为e的正、负电子分别经过直线加速器加速后，从左、右两侧被导入装置送入位于水平面内的圆环形真空管道，且被导入的速度方向与圆环形管道中粗虚线相切。在管道内控制电子转弯的是一系列圆形电磁铁，即图中的A₁、A₂、A₃…A_n，共n个，均匀分布在整个圆周上(图中只示意性地用实线画了几个，其余的用虚线表示)，每个电磁铁内的磁场都是磁感应强度相同的匀强磁场，磁场区域都是直径为d的圆形。改变电磁铁内电流的大小，就可改变磁场的磁感应强度，从而改变电子偏转的角度。经过精确的调整，可使电子在环形管道中沿图中粗虚线所示的轨迹运动，这时电子经过每个电磁铁时射入点和射出点都在圆形匀强磁场区域的同一条直径的两端，如图乙所示。这就为实现正、负电子的对撞作好了准备。

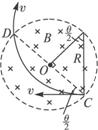
图甲

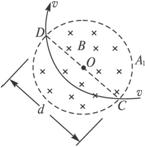
图乙

(1)据相对论知，当1时，物体运动时的能量和静止时的能量之差等于物体的动能。若正、负电子经过直线加速器后的动能均为E₀(能满足vc)，它们对撞后发生湮灭，电子消失，且仅产生一对频率相同的光子，则此光子的频率为多大？(已知普朗克常量为h，真空中的光速为c)?

(2)若电子刚进入直线加速器第一个圆筒时速度大小为v₀,为使电子通过直线加速器后速度为v，加速器所接正弦交流电压的最大值应当多大？

(3)电磁铁内匀强磁场的磁感应强度B为多大？(相邻两电磁铁的间距忽略不计)

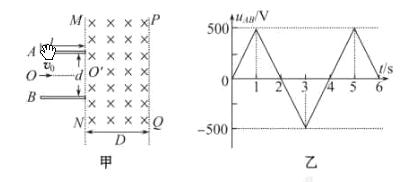
如图甲所示，两平行金属板A、B的板长l=0.20m，板间距d=0.20m，两金属板间加如图乙所示的交变电压，并在两板间形成交变的电场，忽略其边缘效应.在金属板右侧有一方向垂直于纸面向里的匀强磁场．其左右宽度D=0.40 m，上下范围足够大，边界MN和PQ均与金属板垂直.匀强磁场的磁感应强度B=1.0×10T.现从t=0开始，从两极板左端的中点O处以每秒1000个的速率不停地释放出某种带正电的粒子，这些粒子均以v₀=2.0×10m/s的速度沿两板间的中线OO′射入电场，已知带电粒子的比荷=1.0×10C／kg，粒子的重力和粒子间的相互作用都忽略不计，在粒子通过电场区域的极短时间内极板间的电压可以看作不变，sin37°=0.6，cos37°=0.8。问：

（1）t=0时刻进入的粒子，经边界MN射入磁场和射出磁场时两点间的距离是多少？

（2）当AB板间电压满足什么条件时，带电粒子可以进入磁场？在电压变化的第一个周期内有多少个带电的粒子能进入磁场？

（3）何时由O点进入的带电粒子在磁场中运动的时间最长？最长时间为多少？（π≈3）

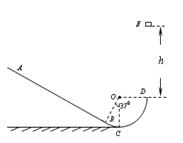
如图所示，在竖直平面内，粗糙的斜面轨道AB的下端与光滑的圆弧轨道BCD相切于B， C是最低点，圆心角∠BOC=37°，D与圆心O等高，圆弧轨道半径R=1.0m，现有一个质量为m=0.2kg可视为质点的小物体，从D点的正上方E点处自由下落，DE距离h＝1.6m，物体与斜面AB之间的动摩擦因数μ=0.5。取sin37^o=0.6，cos37^o=0.8， g=10m/s²。求：

⑴物体第一次通过C点时轨道对物体的支持力F_N的大小；

⑵要使物体不从斜面顶端飞出，斜面的长度L_AB至少要多长；

⑶若斜面已经满足（2）要求，物体从E点开始下落，直至最后在光滑圆弧轨道做周期性运动，在此过程中系统因摩擦所产生的热量Q的大小。

如图所示，在竖直平面内，粗糙的斜面轨道AB的下端与光滑的圆弧轨道BCD相切于B， C是最低点，圆心角∠BOC=37°，D与圆心O等高，圆弧轨道半径R=1.0m，现有一个质量为m=0.2kg可视为质点的小物体，从D点的正上方E点处自由下落，DE距离h＝1.6m，物体与斜面AB之间的动摩擦因数μ=0.5。取sin37^o=0.6，cos37^o=0.8， g=10m/s²。求：

⑴物体第一次通过C点时轨道对物体的支持力F_N的大小；

⑵要使物体不从斜面顶端飞出，斜面的长度L_AB至少要多长；

⑶若斜面已经满足（2）要求，物体从E点开始下落，直至最后在光滑圆弧轨道做周期性运动，在此过程中系统因摩擦所产生的热量Q的大小。

如图所示，在竖直平面内，粗糙的斜面轨道AB的下端与光滑的圆弧轨道BCD相切于B， C是最低点，圆心角∠BOC=37°，D与圆心O等高，圆弧轨道半径R=1.0m，现有一个质量为m=0.2kg可视为质点的小物体，从D点的正上方E点处自由下落，DE距离h＝1.6m，物体与斜面AB之间的动摩擦因数μ=0.5。取sin37o=0.6，cos37o=0.8， g=10m/s2。求：

⑴物体第一次通过C点时轨道对物体的支持力FN的大小；

⑵要使物体不从斜面顶端飞出，斜面的长度LAB至少要多长；

⑶若斜面已经满足⑵要求，物体从E点开始下落，直至最后在光滑圆弧轨道做周期性运动，在此过程中系统因摩擦所产生的热量Q的大小。