题目列表(包括答案和解析)
法拉第电磁感应定律
1．(1)法拉第电磁感应定律：电路中感应电动势的大小________，表达式为E＝________．
(2)当导体在匀强磁场中做切割磁感线的相对运动时产生的感应电动势E＝________，
是B与v之间的夹角．
(3)导体棒绕某一固定转轴旋转切割磁感线，虽然棒上各点的切割速度并不相同，但可用棒上________等效替代切割速度．常用公式E＝________．
2．应用法拉第电磁感应定律时应注意：
(1)E＝________适用于一般回路．若磁通量不随时间均匀变化，则ΔΦ/Δt为Δt时间内通过该回路的磁通量的________．
(2)E＝________，适用于导体各部分以相同的速度切割磁感线的情况，式中L为导线的有效切割长度，为运动方向和磁感线方向的夹角．若v为瞬时速度，则E为________．若v为平均速度，则E为________．
(3)若磁感应强度B不变，回路的面积S发生变化，则E＝________；若回路的面积S不变，磁感应强度B发生变化，则E＝________；若磁感应强度B、回路的面积S都发生变化，则E＝________．
3．要注意严格区分Φ、ΔΦ、ΔΦ/Δt的物理意义
Φ
是指________．ΔΦ是指________．
ΔΦ/Δt是指________．
（1）如图1所示，固定于水平面上的金属框架abcd，处在竖直向下的匀强磁场中。金属棒MN沿框架以速度v向右做匀速运动。框架的ab与dc平行，bc与ab、dc垂直。MN与bc的长度均为l，在运动过程中MN始终与bc平行，且与框架保持良好接触。磁场的磁感应强度为B。
a. 请根据法拉第电磁感应定律
，推导金属棒MN中的感应电动势E；
b. 在上述情景中，金属棒MN相当于一个电源，这时的非静电力与棒中自由电子所受洛伦兹力有关。请根据电动势的定义，推导金属棒MN中的感应电动势E。
（2）为进一步研究导线做切割磁感线运动产生感应电动势的过程，现构建如下情景：如图2所示，在垂直于纸面向里的匀强磁场中，一内壁光滑长为l的绝缘细管MN，沿纸面以速度v向右做匀速运动。在管的N端固定一个电量为q的带正电小球（可看做质点）。某时刻将小球释放，小球将会沿管运动。已知磁感应强度大小为B，小球的重力可忽略。在小球沿管从N运动到M的过程中，求小球所受各力分别对小球做的功。
（1）如图1所示，固定于水平面上的金属框架abcd，处在竖直向下的匀强磁场中。金属棒MN沿框架以速度v向右做匀速运动。框架的ab与dc平行，bc与ab、dc垂直。MN与bc的长度均为l，在运动过程中MN始终与bc平行，且与框架保持良好接触。磁场的磁感应强度为B。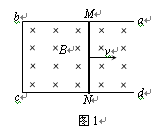
a. 请根据法拉第电磁感应定律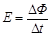
，推导金属棒MN中的感应电动势E；
b. 在上述情景中，金属棒MN相当于一个电源，这时的非静电力与棒中自由电子所受洛伦兹力有关。请根据电动势的定义，推导金属棒MN中的感应电动势E。
（2）为进一步研究导线做切割磁感线运动产生感应电动势的过程，现构建如下情景：如图2所示，在垂直于纸面向里的匀强磁场中，一内壁光滑长为l的绝缘细管MN，沿纸面以速度v向右做匀速运动。在管的N端固定一个电量为q的带正电小球（可看做质点）。某时刻将小球释放，小球将会沿管运动。已知磁感应强度大小为B，小球的重力可忽略。在小球沿管从N运动到M的过程中，求小球所受各力分别对小球做的功。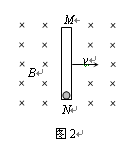
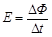，推导金属棒MN中的感应电动势E；
材料二：根据爱因斯坦的狭义相对论观点，相对论的质量速率公式：m=
其中m0表示物体静止时的质量，m表示物体以速率v运动时的质量，c表示光速，若质点的速率远小于光速，则m→m0，质量保持不变，回到牛顿经典力学的观点.
根据以上材料回答问题：
(1)为了保证带电粒子在回旋加速器中如图所示的那样不断被加速，带电粒子的运动周期T1与交变电场的周期T2之间的关系为_____________.
(2)在20世纪30年代末发现，这种回旋加速器加速质子时，最高能量仅能达到20 MeV，要想进一步提高质子的速度很困难，这是因为_________________________________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com