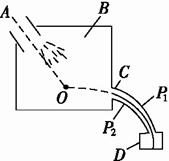
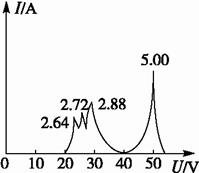
甲                                                      乙

图7

(1)忽略电子的重力;

(2)电子与原子碰撞前,原子静止,原子质量比电子质量大很多,碰撞后原子虽稍微被碰动,但忽略这一能量损失,假定原子未动;

(3)当电子与原子发生弹性碰撞时,电子改变运动方向,但不损失动能;发生非弹性碰撞时,电子损失动能传给原子,使原子内部能量增加.

请根据以上材料和假设回答下列问题:

(1)设速度选择器两极间的电压为U(V)时,允许通过的电子的动能为E_k(eV),写出E_k与U的关系式,设通过选择器的电子轨道半径r=20.0 cm,电极P₁和P₂的间隔d=10.0 mm,两极间场强大小处处相同,都为E;

(2)如果电子枪射出电子的动能E_k=50.0 eV,改变P₁、P₂间电压,测得电流I,得到如图8(乙)所示的I-U图象,图象表明,当电压U为5.00 V、2.88 V、2.72 V、2.64 V时电流出现峰值,试说明在U=5.00 V和U=2.88 V时电子与氦原子碰撞时电子能量的变化.

(3)求氦原子3个激发态的能级E_n.(设基态的能级E₁=0)

已知氢原子基态的电子轨道半径为r₁=0.528×10^-10 m，量子数为n的能级值为E_n=.

（1）求电子在基态轨道上运动的动能.

（2）有一群氢原子处于量子数n=3的激发态，画一张能级图，在图上用箭头标明这些氢原子能发出哪几种光谱线？

（3）计算这几种光谱线中波长最短的波长.（静电力常量k=9×10⁹ N·m²/C²,电子电荷量e=1.6×10^-19 C，普朗克常量h=6.63×10^-34 J·s,真空中光速c=3.00×10⁸ m/s）