
题目列表(包括答案和解析)

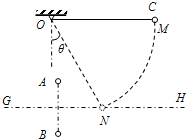 (2008?邵阳模拟)如图所示,在同一条竖直线上,有电荷量均为Q的A、B两个正点电荷,; GH是它们连线的垂直平分线.另有一个带电小球C,质量为m、电荷量为+q(可视为点电荷),被长为L的绝缘轻细线悬挂于O点,现在把小球C拉起到M点,使细线水平且与 A、B处于同一竖直面内,由静止开始释放,小球C向下运动到GH线上的N点时刚好速度为零,此时细线与竖直方向的夹角θ=30°.试求:
(2008?邵阳模拟)如图所示,在同一条竖直线上,有电荷量均为Q的A、B两个正点电荷,; GH是它们连线的垂直平分线.另有一个带电小球C,质量为m、电荷量为+q(可视为点电荷),被长为L的绝缘轻细线悬挂于O点,现在把小球C拉起到M点,使细线水平且与 A、B处于同一竖直面内,由静止开始释放,小球C向下运动到GH线上的N点时刚好速度为零,此时细线与竖直方向的夹角θ=30°.试求: (2008?福建模拟)如图所示,在NOQ范围内有垂直于纸面向里的匀强磁场I,在MOQ范围内有垂直于纸面向外的匀强磁场Ⅱ,M、O、N在一条直线上,∠MOQ=60°,这两个区域磁场的磁感应强度大小均为B.离子源中的离子带电荷量为+q,质量为m,通过小孔O1进入两板间电压为U的加速电场区域(可认为初速度为零),离子经电场加速后由小孔O2射出,再从O点进入磁场区域I,此时速度方向沿纸面垂直于磁场边界MN不计离子的重力.
(2008?福建模拟)如图所示,在NOQ范围内有垂直于纸面向里的匀强磁场I,在MOQ范围内有垂直于纸面向外的匀强磁场Ⅱ,M、O、N在一条直线上,∠MOQ=60°,这两个区域磁场的磁感应强度大小均为B.离子源中的离子带电荷量为+q,质量为m,通过小孔O1进入两板间电压为U的加速电场区域(可认为初速度为零),离子经电场加速后由小孔O2射出,再从O点进入磁场区域I,此时速度方向沿纸面垂直于磁场边界MN不计离子的重力.
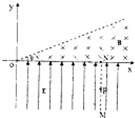 (2013?安庆二模)如图所示,在xoy平面的第四象限内存在沿y轴正方向的匀强磁场,场强大小为E,第一象限存在一有界匀强磁场,方向垂直于xoy平面向里,磁感应强度为B,磁场上边界与x轴正向夹角θ=30°,直线MN与y轴平行,N点坐标为(L,0),现从MN上的P点无初速度释放质量为m,电荷量为q的带正电粒子,不计粒子的重力,求:
(2013?安庆二模)如图所示,在xoy平面的第四象限内存在沿y轴正方向的匀强磁场,场强大小为E,第一象限存在一有界匀强磁场,方向垂直于xoy平面向里,磁感应强度为B,磁场上边界与x轴正向夹角θ=30°,直线MN与y轴平行,N点坐标为(L,0),现从MN上的P点无初速度释放质量为m,电荷量为q的带正电粒子,不计粒子的重力,求:湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com