
题目列表(包括答案和解析)
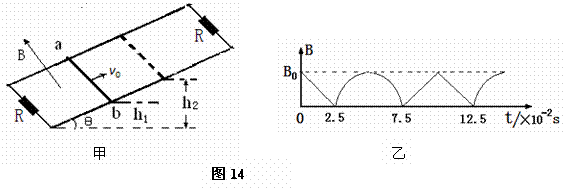
 横截面积分别为SA=2.0×10-3m2、SB=1.0×10-3m2的汽缸A、B竖直放置,底部用细管连通,用质量分别为mA=4.0kg、mB=2.0kg的活塞封闭一定质量的气体,气缸A中有定位卡.当气体温度为27℃时,活塞A恰与定位卡环接触,此时封闭气体的体积为V0=300mL,外界大气压强为P0=1.0×105Pa.(g=10m/s2)
横截面积分别为SA=2.0×10-3m2、SB=1.0×10-3m2的汽缸A、B竖直放置,底部用细管连通,用质量分别为mA=4.0kg、mB=2.0kg的活塞封闭一定质量的气体,气缸A中有定位卡.当气体温度为27℃时,活塞A恰与定位卡环接触,此时封闭气体的体积为V0=300mL,外界大气压强为P0=1.0×105Pa.(g=10m/s2) 如图所示,真空中有两个点电荷Q1=+4.0×10-8C和Q2=-1.0×10-8C,分别固定在x坐标轴的x=0和x=6cm位置上.
如图所示,真空中有两个点电荷Q1=+4.0×10-8C和Q2=-1.0×10-8C,分别固定在x坐标轴的x=0和x=6cm位置上. (2011?南京模拟)如图所示,一个质量为m=2.0×10-11Kg电荷q=1.0×10-5C的带正电微粒,重力可忽略不计,从静止开始经电压U1=100V的电场加速后,水平进入两平行金属板间的偏转电场,偏转电场的电压U2=100V,金属板长L=20cm,两板间距d=10
(2011?南京模拟)如图所示,一个质量为m=2.0×10-11Kg电荷q=1.0×10-5C的带正电微粒,重力可忽略不计,从静止开始经电压U1=100V的电场加速后,水平进入两平行金属板间的偏转电场,偏转电场的电压U2=100V,金属板长L=20cm,两板间距d=10| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com