
题目列表(包括答案和解析)
 如图所示,粗细均匀的电阻丝制成的圆环上有A、B、C三个点,已知,A、B两点等分圆环的周长,弧BC是弧AB的
如图所示,粗细均匀的电阻丝制成的圆环上有A、B、C三个点,已知,A、B两点等分圆环的周长,弧BC是弧AB的| 1 | 4 |
 如图所示,粗细均匀的玻璃管,当温度为27℃时,封闭在管内的空气柱AB长为30cm,BC长为10cm,管内水银柱水平部分CD长为18cm,竖直部分DE长为15cm,外界大气压强为75cmHg,问:要使水平管内没有水银柱,温度至少要升高到多少℃?
如图所示,粗细均匀的玻璃管,当温度为27℃时,封闭在管内的空气柱AB长为30cm,BC长为10cm,管内水银柱水平部分CD长为18cm,竖直部分DE长为15cm,外界大气压强为75cmHg,问:要使水平管内没有水银柱,温度至少要升高到多少℃?| p1V1 |
| T1 |
| p2V2 |
| T2 |
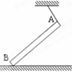 如图所示,粗细均匀的长直杆,一端用悬绳挂在天花板上,另一端搁在地面上而处于静止状态,则该杆受力情况是:( )
如图所示,粗细均匀的长直杆,一端用悬绳挂在天花板上,另一端搁在地面上而处于静止状态,则该杆受力情况是:( )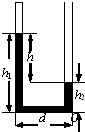 如图所示,粗细均匀的U形管,左管封闭一段空气柱,两侧水银面高度差为h,U形管两管间宽度为d,且d<h.现将U形管以O点为轴顺时针旋转90°,至两平行管水平,并保持U形管在竖直面内.设温度不变,管的直径可忽略不计,水银没有溢出,则下列说法中正确的是( )
如图所示,粗细均匀的U形管,左管封闭一段空气柱,两侧水银面高度差为h,U形管两管间宽度为d,且d<h.现将U形管以O点为轴顺时针旋转90°,至两平行管水平,并保持U形管在竖直面内.设温度不变,管的直径可忽略不计,水银没有溢出,则下列说法中正确的是( ) (2010?长宁区一模)如图所示,粗细均匀的细直玻璃管上端封闭,开口端竖直向下插入水银槽中,管内封闭有一定质量的理想气体,玻璃管露出水银槽液面的长度为L=40cm,管内外水银面高度差为h=8cm.现使管缓慢转过θ=37°角,保持玻璃管在水银槽液面上方的长度L不变,外界大气压强不变,这时( )
(2010?长宁区一模)如图所示,粗细均匀的细直玻璃管上端封闭,开口端竖直向下插入水银槽中,管内封闭有一定质量的理想气体,玻璃管露出水银槽液面的长度为L=40cm,管内外水银面高度差为h=8cm.现使管缓慢转过θ=37°角,保持玻璃管在水银槽液面上方的长度L不变,外界大气压强不变,这时( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com