
题目列表(包括答案和解析)
设地面附近重力加速度为g,地球半径为R,人造地球卫星圆形轨道半径为r,那么以下说法中正确的是
[ ]
A.卫星在轨道上向心加速度大小为![]()
B.卫星运行的线速度大小为![]()
C.卫星运行的角速度大小为![]()
D.卫星运行的周期为2π![]()
“重力探矿”是常用的探测石油矿藏的方法之一。其原理可简述如下:如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为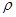 ;石油密度远小于
;石油密度远小于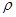 ,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。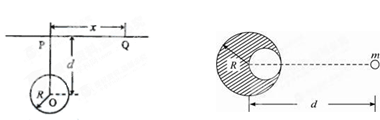
(1)“重力探矿”利用了“割补法”原理:如图所示,在一个半径为R、质量为M的均匀球体中,紧贴球的边缘挖去一个半径为R/2的球形空穴后,剩余的阴影部分对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大?
(2)设球形空腔体积为V,球心深度为d(远小于地球半径),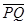 =x,利用“割补法”原理:如果将近地表的球形空腔填满密度为
=x,利用“割补法”原理:如果将近地表的球形空腔填满密度为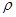 的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力
的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力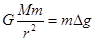 来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值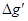 (
(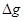 在OP方向上的分量)
在OP方向上的分量)
(3)若在水平地面上半径L的范围内发现:重力加速度反常值在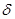 与
与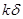 (k>1)(
(k>1)(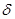 为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
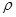 ;石油密度远小于
;石油密度远小于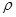 ,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
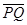 =x,利用“割补法”原理:如果将近地表的球形空腔填满密度为
=x,利用“割补法”原理:如果将近地表的球形空腔填满密度为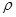 的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力
的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力 来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值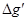 (
(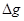 在OP方向上的分量)
在OP方向上的分量)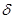 与
与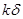 (k>1)(
(k>1)(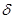 为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。设地球的半径为R,地表附近重力加速度为g,一颗质量为m离地面高度也为R的人造地球卫星绕地球做匀速圆周运动,则
[ ]
A.卫星的加速度大小为![]()
B.卫星受万有引力的大小为![]()
C.卫星线速度的大小为![]()
D.卫星的角速度为![]()
 ,r为物体离地心的距离.设地球半径为r,地球表面重力加速度为g,忽略空气阻力的影响,试根据所学的知识,推导第二宇宙速度的表达式(用r、g表示).
,r为物体离地心的距离.设地球半径为r,地球表面重力加速度为g,忽略空气阻力的影响,试根据所学的知识,推导第二宇宙速度的表达式(用r、g表示).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com