某同学在用单摆测定重力加速度的实验中,测量5种不同摆长情况下单摆的振动周期,记录结果见下表:
| L/m |
0.5 |
0.8 |
0.9 |
1.0 |
1.2 |
| T/s |
1.42 |
1.79 |
1.90 |
2.00 |
2.20 |
| T2/s2 |
2.02 |
3.20 |
3.61 |
4.00 |
4.84 |
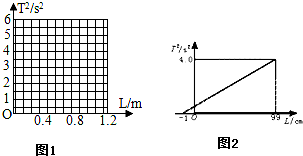
(1)以L为横坐标,T
2为纵坐标,作出T
2-L图线(如图1),并利用此图线求出重力加速度g=
9.87
9.87
m/s
2.(取π
2=9.87)?
(2)若某同学测定的g的数值比当地公认值大,造成的原因可能是
CEF
CEF
;
A、摆球质量太大了;
B、摆长太长了;
C、摆角太大了(摆角仍小于10°);
C、量摆长时从悬点量到球的最下端;
D、计算摆长时忘记把小球半径加进去;
E、摆球不是在竖直平面内做简谐振动,而是做圆锥摆运动;
F、计算周期时,将(n-1)次全振动误记为n次全振动;
(3)若某同学根据实验数据作出的图象如图2所示.则造成图象不过坐标原点的原因是
漏测小球的半径r
漏测小球的半径r
;?
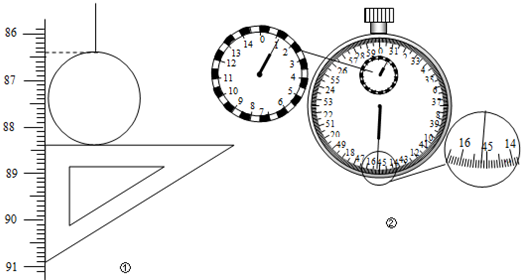
(4)如果已知摆球直径为2.00cm,让刻度尺的零点对准摆线的悬点,摆线竖直下垂.如图①所示,那么单摆摆长是
0.8740
0.8740
m.如果测定了40次全振动所用时间如图②中秒表所示,单摆的运动周期是
1.88
1.88
s.

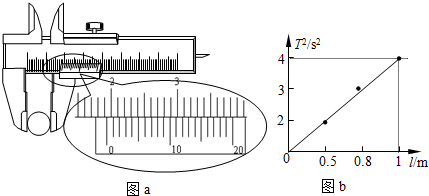
 某同学在“用单摆测定重力加速度”的实验中,测量5种不同摆长l的情况下单摆振动的周期T,并用所测得的数据在如图所示的坐标系中描出5个点.请你在图8中画出T2-l的图象,根据这些点可求出重力加速度的测量值为
某同学在“用单摆测定重力加速度”的实验中,测量5种不同摆长l的情况下单摆振动的周期T,并用所测得的数据在如图所示的坐标系中描出5个点.请你在图8中画出T2-l的图象,根据这些点可求出重力加速度的测量值为
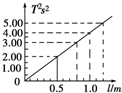 某同学在用单摆测定重力加速度的实验中,测量4种不同摆长情况单摆的振动周期,获得4组数据,以T2为纵轴、l为横轴作出的T2-l关系图象如图,根据此图象回答问题:
某同学在用单摆测定重力加速度的实验中,测量4种不同摆长情况单摆的振动周期,获得4组数据,以T2为纵轴、l为横轴作出的T2-l关系图象如图,根据此图象回答问题:
