
题目列表(包括答案和解析)
 民用航空客机的机舱,除了有正常的舱门和舷梯连接,供旅客上下飞机以外,还配有紧急出口.发生意外情况的飞机在着陆后,打开紧急出口的舱门后,会自动生成一个气囊,由斜面部分AC和水平部分CD构成,乘客可沿该气囊安全地滑行到地面,如图所示.某机舱离气囊底端的竖直高度AB=3.0m,气囊构成的斜面长AC=5.0m.质量m=60kg的乘客从气囊上由静止开始滑下,最后滑上水平部分上的E点静止.已知乘客与气囊动摩擦因数为μ=0.60,不计空气阻力,取g=10m/s2.求:
民用航空客机的机舱,除了有正常的舱门和舷梯连接,供旅客上下飞机以外,还配有紧急出口.发生意外情况的飞机在着陆后,打开紧急出口的舱门后,会自动生成一个气囊,由斜面部分AC和水平部分CD构成,乘客可沿该气囊安全地滑行到地面,如图所示.某机舱离气囊底端的竖直高度AB=3.0m,气囊构成的斜面长AC=5.0m.质量m=60kg的乘客从气囊上由静止开始滑下,最后滑上水平部分上的E点静止.已知乘客与气囊动摩擦因数为μ=0.60,不计空气阻力,取g=10m/s2.求: 质量m=60kg的消防队员,从一根竖直的长直杆上由静止滑下,经t=2.0s着地.消防队员整个下滑过程的v-t图象如图所示.求:
质量m=60kg的消防队员,从一根竖直的长直杆上由静止滑下,经t=2.0s着地.消防队员整个下滑过程的v-t图象如图所示.求: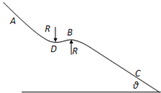 如图是一高山滑雪运动场中的滑道,BD附近是很小的一段曲道,可认为是半径均为R=40m的两圆滑连接的圆形滑道,B点和D点是两圆弧的最高点和最低点,圆弧长度远小于斜面BC长度,一个质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑道滑下,刚好能从B点水平抛出,已知AB两点间的高度差为h=25m,滑道的倾角θ=37°,取g=10m/s2.求:
如图是一高山滑雪运动场中的滑道,BD附近是很小的一段曲道,可认为是半径均为R=40m的两圆滑连接的圆形滑道,B点和D点是两圆弧的最高点和最低点,圆弧长度远小于斜面BC长度,一个质量m=60kg的高山滑雪运动员,从A点由静止开始沿滑道滑下,刚好能从B点水平抛出,已知AB两点间的高度差为h=25m,滑道的倾角θ=37°,取g=10m/s2.求: 如图所示,一位质量m=60kg,参加“挑战极限运动”的业余选手,要越过一宽为s=2.5m的水沟后跃上高为h=2.0m的平台.他采用的方法是:手握一根长L=3.25m的轻质弹性杆一端,从A点由静止开始加速助跑,至B点时杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直状态,人的重心在杆的顶端,此刻人放开杆水平飞出并趴落到平台上,运动过程中空气阻力可忽略不计.(g取10m/s2)求:
如图所示,一位质量m=60kg,参加“挑战极限运动”的业余选手,要越过一宽为s=2.5m的水沟后跃上高为h=2.0m的平台.他采用的方法是:手握一根长L=3.25m的轻质弹性杆一端,从A点由静止开始加速助跑,至B点时杆另一端抵在O点的阻挡物上,接着杆发生形变,同时人蹬地后被弹起,到达最高点时杆处于竖直状态,人的重心在杆的顶端,此刻人放开杆水平飞出并趴落到平台上,运动过程中空气阻力可忽略不计.(g取10m/s2)求: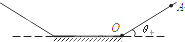 滑雪运动常在两个斜面和一个平面的组合场地中进行,我们把它简化为理想情景如图所示.假定运动员和滑板的总质量为m=60kg,从O点以初速度v0=2m/s冲上倾角为θ=37°的斜面,则经过t=5/24s时间第一次冲到斜面的最高
滑雪运动常在两个斜面和一个平面的组合场地中进行,我们把它简化为理想情景如图所示.假定运动员和滑板的总质量为m=60kg,从O点以初速度v0=2m/s冲上倾角为θ=37°的斜面,则经过t=5/24s时间第一次冲到斜面的最高湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com