
题目列表(包括答案和解析)
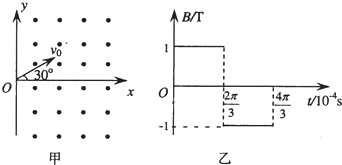
 如图甲所示,空间存在着以x=0平面为理想分界面的两个匀强磁场,左右两边磁场的磁感应强度分别为B1和B2,且B1:B2=4:3.方向如图,现在原点O处有一静止的中性粒子,突然分裂成两个带电粒子a和b,已知a带正电荷,分裂时初速度方向沿x轴正方向.若a粒子在第4次经过y轴时,恰与b粒子相遇.(1)在图乙中,画出a粒子的运动轨迹及用字母c标出a、b两粒子相遇的位置
如图甲所示,空间存在着以x=0平面为理想分界面的两个匀强磁场,左右两边磁场的磁感应强度分别为B1和B2,且B1:B2=4:3.方向如图,现在原点O处有一静止的中性粒子,突然分裂成两个带电粒子a和b,已知a带正电荷,分裂时初速度方向沿x轴正方向.若a粒子在第4次经过y轴时,恰与b粒子相遇.(1)在图乙中,画出a粒子的运动轨迹及用字母c标出a、b两粒子相遇的位置| q |
| m |
| 4π |
| 3 |
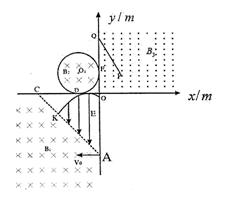
如图—26所示,在xoy坐标系中分布着四个有界场区,在第三象限的AC左下方存在垂直纸面向里的匀强磁场B1=0.5T,AC是直线y=-x—0.425(单位:m)在第三象限的部分,另一沿y轴负向的匀强电场左下边界也为线段AC的一部分,右边界为y轴,上边界是满足![]() (单位:m)的抛物线的一部分,电场强度E=2.5N/C。在第二象限有一半径为r=0.1m的圆形磁场区域,磁感应强度B2=1T,方向垂直纸面向里,该区域同时与x轴、y轴相切,切点分别为D、F,在第一象限的整个空间存在垂直纸面向外的匀强磁场,磁感应强度B3=1T,另有一厚度不计的挡板PQ垂直纸面放置,其下端坐标P(0.1m,0.1m),上端Q在y轴上,且∠PQF=30°现有大量m=1×10-6kg,q=-2×10-4C的粒子(重力不计)同时从A点沿x轴负向以v0射入,且v0取0<v0<20m/s之=4-4d
(单位:m)的抛物线的一部分,电场强度E=2.5N/C。在第二象限有一半径为r=0.1m的圆形磁场区域,磁感应强度B2=1T,方向垂直纸面向里,该区域同时与x轴、y轴相切,切点分别为D、F,在第一象限的整个空间存在垂直纸面向外的匀强磁场,磁感应强度B3=1T,另有一厚度不计的挡板PQ垂直纸面放置,其下端坐标P(0.1m,0.1m),上端Q在y轴上,且∠PQF=30°现有大量m=1×10-6kg,q=-2×10-4C的粒子(重力不计)同时从A点沿x轴负向以v0射入,且v0取0<v0<20m/s之=4-4d
之间的一系列连续值,并假设任一速度的粒子数占入射粒子总数的比例相
同。
(1)求所有粒子从第三象限穿越x轴时的速度;
(2)设从A点发出的粒子总数为N,求最终打在挡板PQ右侧的粒子数N'.
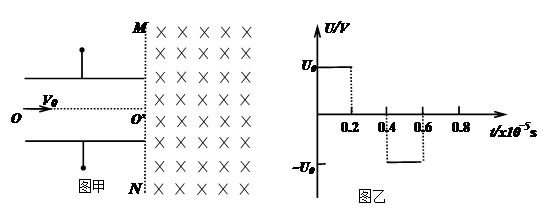
(15分)如图甲所示,两平行金属板间接有如图乙所示的随时间t变化的交流电压u,金属板间电场可看做均匀、且两板外无电场,板长L=0.2m,板间距离d=0.1m,在金属板右侧有一边界为MN的匀强磁场,MN与两板中线OO′ 垂直,磁感应强度B=5×10-3T,方向垂直纸面向里。现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的比荷![]() =108C/kg,重力忽略不计,在0-0.8×10-5s时间内两板间加上如图乙所示的电压(不考虑极板边缘的影响)。已知t = 0时刻进入两板间的带电粒子恰好在0.2×10-5s时刻经极板边缘射入磁场。(不考虑粒子间相互影响及返回板间的情况)。
=108C/kg,重力忽略不计,在0-0.8×10-5s时间内两板间加上如图乙所示的电压(不考虑极板边缘的影响)。已知t = 0时刻进入两板间的带电粒子恰好在0.2×10-5s时刻经极板边缘射入磁场。(不考虑粒子间相互影响及返回板间的情况)。
求:
(1)求两板间的电压U0
(2)0-0.2×10-5s时间内射入两板间的带电粒子都能够从磁场右边界射出,求磁场的最大宽度
(3)若以MN与两板中线OO′ 垂直的交点为坐标原点,水平向右为x轴,竖直向上为y轴建立二维坐标系,请写出在0.3×10-5s时刻射入两板间的带电粒子进入磁场和离开磁场(此时,磁场只有左边界,没有右边界)时的位置坐标。
(4)两板间电压为0,请设计一种方案:让向右连续发射的粒子流沿两板中线OO′射入,经过右边的待设计的磁场区域后,带电粒子又返回粒子源。
(15分)如图甲所示,两平行金属板间接有如图乙所示的随时间t变化的交流电压u,金属板间电场可看做均匀、且两板外无电场,板长L=0.2m,板间距离d=0.1m,在金属板右侧有一边界为MN的匀强磁场,MN与两板中线OO′ 垂直,磁感应强度 B=5×10-3T,方向垂直纸面向里。现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的比荷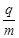 =108C/kg,重力忽略不计,在0-0.8×10-5s时间内两板间加上如图乙所示的电压(不考虑极板边缘的影响)。已知t = 0时刻进入两板间的带电粒子恰好在0.2×10-5s时刻经极板边缘射入磁场。(不考虑粒子间相互影响及返回板间的情况)。
=108C/kg,重力忽略不计,在0-0.8×10-5s时间内两板间加上如图乙所示的电压(不考虑极板边缘的影响)。已知t = 0时刻进入两板间的带电粒子恰好在0.2×10-5s时刻经极板边缘射入磁场。(不考虑粒子间相互影响及返回板间的情况)。
求: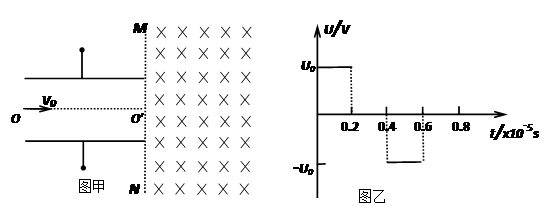
(1)求两板间的电压U0
(2)0-0.2×10-5s时间内射入两板间的带电粒子都能够从磁场右边界射出,求磁场的最大宽度
(3)若以MN与两板中线OO′ 垂直的交点为坐标原点,水平向右为x轴,竖直向上为y轴建立二维坐标系,请写出在0.3×10-5s时刻射入两板间的带电粒子进入磁场和离开磁场(此时,磁场只有左边界,没有右边界)时的位置坐标。
(4)两板间电压为0,请设计一种方案:让向右连续发射的粒子流沿两板中线OO′射入,经过右边的待设计的磁场区域后,带电粒子又返回粒子源。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com