练习册

  • 练习册
  • 试题
    16．如图一所示.竖直面上有两根电阻不计的光滑金属导轨平行固定放置.间距d为0.5 m.上端通过导线与阻值为2 W的电阻R连接.下端通过导线与阻值为4 W的小灯泡L连接.在CDEF矩形区域内有水平向外的匀强磁场.磁感应强度B随时间变化如图二所示.CE长为2 m.在t＝0时.电阻2 W的金属棒以某一初速度从AB位置紧贴导轨向下运动.当金属棒从AB位置运动到EF位置过程中.小灯泡的亮度没有发生变化.g取10m/s2.求: (1)通过小灯泡的电流强度 (2)金属棒的质量 (3)t=0.25s时金属棒两端的电势差 (4)金属棒从AB位置运动到EF位置过程中.电阻R中的焦耳热 【查看更多】

     

    题目列表(包括答案和解析)

    精英家教网如图a所示，竖直平面内有两根光滑且不计电阻的长平行金属导轨，间距L．导轨间的空间内存在垂直导轨平面的匀强磁场．将一质量m、电阻R的金属杆水平靠在导轨处上下运动，与导轨接触良好．
    （1）若磁感应强度随时间变化满足B=kt，k为已知非零常数．金属杆在距离导轨顶部L处释放，则何时释放，会获得向上的加速度．
    （2）若磁感应强度随时间变化满足B=
    B0c+dt2
    ，B0、c、d均为已知非零常数．为使金属杆中没有感应电流产生，从t=0时刻起，金属杆应在外力作用下做何种运动？列式说明．
    （3）若磁感应强度恒定为B0，静止释放金属杆．对比b图中从铝管顶部静止释放磁性小球在铝管中的下落．试从能量角度用文字分析两图中的共同点．

    查看答案和解析>>

    如图所示，水平面上有两根电阻不计的光滑金属导轨平行固定放置，间距d 为0.5m，金属导轨右端通过导线与阻值为4Ω的小灯泡L连接；在CDEF矩形区域内有竖直向上匀强磁场，CE长为2m，CDEF区域内磁场的磁感应强度B随时间t变化如图所示；在t=0s时，一阻值为1Ω的金属棒在恒力F作用下由静止开始从AB位置沿导轨向右运动，在金属棒从AB位置运动到EF位置过程中，小灯泡的亮度始终没有发生变化。求：
    （1）通过的小灯泡的电流大小。
    （2）恒力F的大小。
     

    查看答案和解析>>

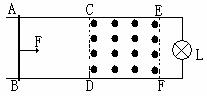
    如图a所示，竖直平面内有两根光滑且不计电阻的长平行金属导轨，间距L。导轨间的空间内存在垂直导轨平面的匀强磁场。将一质量m、电阻R的金属杆水平靠在导轨处上下运动，与导轨接触良好。

    （1）若磁感应强度随时间变化满足B=kt，k为已知非零常数。金属杆在距离导轨顶部L处释放，则何时释放，会获得向上的加速度。

    （2）若磁感应强度随时间变化满足，B0、c、d均为已知非零常数。为使金属杆中没有感应电流产生，从t=0时刻起，金属杆应在外力作用下做何种运动？列式说明。

    （3）若磁感应强度恒定为B0，静止释放金属杆。对比b图中从铝管顶部静止释放磁性小球在铝管中的下落。试从能量角度用文字分析两图中的共同点。

     


    查看答案和解析>>

    如图14所示，竖直放置的两根足够长的光滑金属导轨相距为L，导轨的两端分别与电源(串有一滑动变阻器R)、定值电阻、电容器(原来不带电)和开关S相连.整个空间充满了垂直于导轨平面向外的匀强磁场，其磁感应强度的大小为B.一质量为m，电阻不计的金属棒ab横跨在导轨上.已知电源电动势为E，内阻为r，电容器的电容为C，定值电阻的阻值为R0，不计导轨的电阻.

    图14

    (1)当S接1时，金属棒ab在磁场中恰好保持静止，则滑动变阻器接入电路的阻值R为多大?

    (2)当S接2后，金属棒ab从静止开始下落，下落距离s时达到稳定速度，则此稳定速度的大小为多大?下落s的过程中所需的时间为多少?

    (3)先把开关S接通2，待ab达到稳定速度后，再将开关S接到3.试通过推导，说明ab棒此后的运动性质如何?求ab再下落距离s时，电容器储存的电能是多少?(设电容器不漏电，此时电容器还没有被击穿)

    查看答案和解析>>

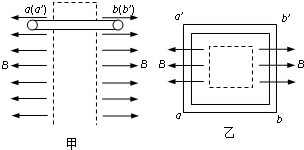    如图甲所示，在虚线框两侧区域存在有大小为B、方向分别为水平向左和水平向右的匀强磁场．用薄金属条制成的闭合正方形框aa′b′b边长为L，质量为m，电阻为R．现将金属方框水平地放在磁场中，aa′边、bb′边分别位于左、右两边的磁场中，方向均与磁场方向垂直，乙图是从上向下看的俯视图．金属方框由静止开始下落，其平面在下落过程中保持水平（不计空气阻力）．
    （1）请根据乙图指出下落时方框中感应电流的方向；
    （2）求方框下落的最大速度vm（设磁场区域在竖直方向足够长）；
    （3）当方框下落的加速度为 
    g2
     时，求方框内感应电流的功率P；
    （4）从静止开始经过时间t，方框下落高度为h，速度为vt（vt＜vm）．若在这段时间内感应电流做的功与一恒定电流I0在t时间内在该框内做的功相同，求恒定电流I0的表达式．

    查看答案和解析>>


    同步练习册答案