
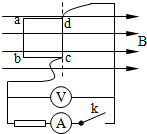
如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.
(1)将开关合到位置1,待螺线管A中的电流稳定后,再将K从位置1拨到位置2,测得D的最大偏转距离为d
m,已知冲击电流计的磁通灵敏度为D
φ,D
φ=
,式中△?为单匝试测线圈磁通量的变化量.则试测线圈所在处磁感应强度B=
;若将K从位置1拨到位置2的过程所用的时间为△t,则试测线圈P中产生的平均感应电动势ε=
.
(2)调节可变电阻R,多次改变电流并拨动K,得到A中电流I和磁感应强度B的数据,见右表.由此可得,螺线管A内部在感应强度B和电流I的关系为B=
.
| 实验次数 |
I(A) |
B(×10-3T) |
| 1 |
0.5 |
0.62 |
| 2 |
1.0 |
1.25 |
| 3 |
1.5 |
1.88 |
| 4 |
2.0 |
2.51 |
| 5 |
2.5 |
3.12 |
(3)(多选题)为了减小实验误差,提高测量的准确性,可采取的措施有
(A)适当增加试测线圈的匝数N
(B)适当增大试测线圈的横截面积S
(C)适当增大可变电阻R的阻值
(D)适当拨长拨动开关的时间△t.

 如图所示正方形线框abcd边长L=0.1m,每边电阻1Ω,在磁感应强度B=0.3T的匀强磁场中绕cd以每分钟
如图所示正方形线框abcd边长L=0.1m,每边电阻1Ω,在磁感应强度B=0.3T的匀强磁场中绕cd以每分钟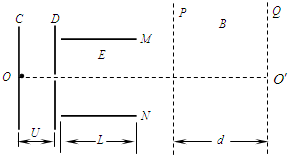 如图,某带电粒子由静止经C、D间电压U=1×103V加速后,沿两水平金属板M、N中心线OO′射入.已知两金属板长L=0.2m,板间有一沿竖直方向的匀强电场(板外无电场),场强E=1×104V/m.在板右端有一垂直纸面的匀强磁场,磁感应强度B=0.3T,P、Q是磁场的左右两个竖直理想边界,粒子在磁场中运动的最长时间为t=1.5×10-4S.(粒子重力不计,π≈3)求:
如图,某带电粒子由静止经C、D间电压U=1×103V加速后,沿两水平金属板M、N中心线OO′射入.已知两金属板长L=0.2m,板间有一沿竖直方向的匀强电场(板外无电场),场强E=1×104V/m.在板右端有一垂直纸面的匀强磁场,磁感应强度B=0.3T,P、Q是磁场的左右两个竖直理想边界,粒子在磁场中运动的最长时间为t=1.5×10-4S.(粒子重力不计,π≈3)求: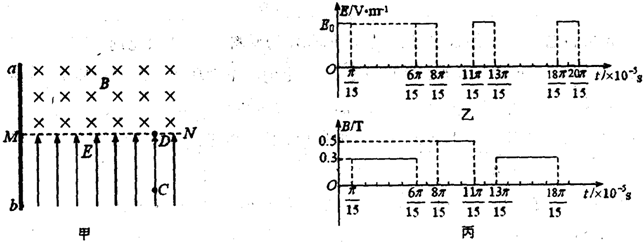
 如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.
如图所示是测量通电螺线管A内部磁感应强度B及其与电流I关系的实验装置.将截面积为S、匝数为N的小试测线圈P置于螺线管A中间,试测线圈平面与螺线管的轴线垂直,可认为穿过该试测线圈的磁场均匀.将试测线圈引线的两端与冲击电流计D相连.拨动双刀双掷换向开关K,改变通入螺线管的电流方向,而不改变电流大小,在P中产生的感应电流引起D的指针偏转.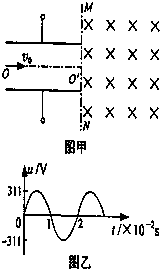 如图(甲)所示,两平行金属板间接有如图(乙)所示交变电压u,两板间电场可看作是均匀的,且两板外无电场.已知极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板中线OO′垂直,磁感应强度B=5×10-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷q/m=108C/kg,
如图(甲)所示,两平行金属板间接有如图(乙)所示交变电压u,两板间电场可看作是均匀的,且两板外无电场.已知极板长L=0.2m,板间距离d=0.2m,在金属板右侧有一边界为MN的区域足够大的匀强磁场,MN与两板中线OO′垂直,磁感应强度B=5×10-3T,方向垂直纸面向里.现有带正电的粒子流沿两板中线OO′连续射入电场中,已知每个粒子的速度v0=105m/s,比荷q/m=108C/kg,