
题目列表(包括答案和解析)
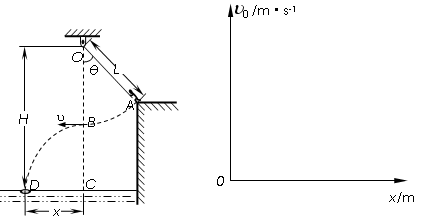
如图所示,质量m=50kg的运动员(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点有一只救生圈,O、A、C、D各点均在同一竖直面内。若运动员抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定初速度![]() 跃出,当摆到O点正下方的B点时松开手,最终恰能落在救生圈内。(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
跃出,当摆到O点正下方的B点时松开手,最终恰能落在救生圈内。(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
(1)运动员经过B点时速度的大小![]() ;
;
(2)运动员从台阶上A点跃出时的动能Ek;
(3)若初速度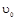 不一定,且使运动员最终仍能落在救生圈内,则救生圈离C点距离x将随运动员离开A点时初速度
不一定,且使运动员最终仍能落在救生圈内,则救生圈离C点距离x将随运动员离开A点时初速度![]() 的变化而变化。试在下面坐标系中粗略作出x-
的变化而变化。试在下面坐标系中粗略作出x-![]() 的图像,并标出图线与x轴的交点。
的图像,并标出图线与x轴的交点。
|
如图所示,质量m=50kg的运动员(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点有一只救生圈,O、A、C、D各点均在同一竖直面内。若运动员抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定初速度 跃出,当摆到O点正下方的B点时松开手,最终恰能落在救生圈内。(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
跃出,当摆到O点正下方的B点时松开手,最终恰能落在救生圈内。(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
(1)运动员经过B点时速度的大小 ;
;
(2)运动员从台阶上A点跃出时的动能Ek;
(3)若初速度 不一定,且使运动员最终仍能落在救生圈内,则救生圈离C点距离x将随运动员离开A点时初速度
不一定,且使运动员最终仍能落在救生圈内,则救生圈离C点距离x将随运动员离开A点时初速度 的变化而变化。试在下面坐标系中粗略作出x-
的变化而变化。试在下面坐标系中粗略作出x- 的图像,并标出图线与x轴的交点。
的图像,并标出图线与x轴的交点。
|

如图所示,质量m=50kg的运动员(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=5.0m处的D点有一只救生圈,O、A、C、D各点均在同一竖直面内。若运动员抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定初速度跃出,当摆到O点正下方的B点时松开手,最终恰能落在救生圈内。(sin37°=0.6,cos37°=0.8,g=10m/s2)求: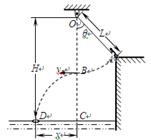
(1)运动员经过B点时速度 的大小;
的大小;
(2)运动员经过B点时绳子的拉力大小;
(3)运动员从A点跃出时的动能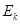 。
。
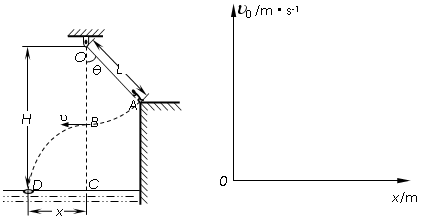
(8分)如图所示,质量m=50kg的运动员(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=4.8m处的D点有一只救生圈,O、A、C、D各点均在同一竖直面内。若运动员抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定初速度![]() 跃出,当摆到O点正下方的B点时松开手,最终恰能落在救生圈内。(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
跃出,当摆到O点正下方的B点时松开手,最终恰能落在救生圈内。(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
(1)运动员经过B点时速度的大小![]() ;
;
(2)运动员从台阶上A点跃出时的动能Ek;
(3)若初速度![]() 不一定,且使运动员最终仍能落在救生圈内,则救生圈离C点距离x将随运动员离开A点时初速度
不一定,且使运动员最终仍能落在救生圈内,则救生圈离C点距离x将随运动员离开A点时初速度![]() 的变化而变化。试在下面坐标系中粗略作出x-
的变化而变化。试在下面坐标系中粗略作出x-![]() 的图像,并标出图线与x轴的交点。
的图像,并标出图线与x轴的交点。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com