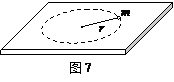
如图7所示，在光滑水平面上，一质量为m＝0.20kg的小球在绳的拉力作用下做半径为r＝1.0m的匀速圆周运动。已知小球运动的线速度大小为v＝2.0m/s，求：

（1）小球运动的周期；

（2）小球做匀速圆周运动时，绳对它的拉力大小。

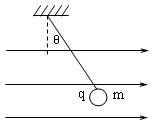如图7所示，在匀强电场中，一质量为m，带电量q的小球（看成质点）被长为L的细线吊起，当球静止时，细线与竖直方向的夹角为θ，则

(1).判断小球带电的电性。

(2).计算电场场强的大小。

关于“验证动量守恒定律”的实验，请完成下列的三个问题：
（1）（3分）如图7所示，在做“验证动量守恒定律”的实验时，实验必须要求满足的条件是：
A．斜槽轨道必须是光滑的
B．斜槽轨道末端的切线是水平的
C．入射球每次都要从同一高度由静止滚下                           
D．若入射小球质量为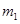，被碰小球质量为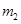，则>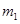    
 
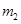
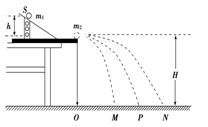
（2）．（2分）利用“碰撞实验器”可以验证动量守恒定律，即研究两个小球在轨道水平部分碰撞前后的动量关系．图中O点是小球抛出点在地面上的垂直投影．实验时，先让入射球m₁多次从斜轨上的S位置静止释放，找到其平均落地点的位置P，测量出平抛的射程OP. 然后，把被碰小球m₂静置于轨道的水平部分，再将入射小球m₁从斜轨上的S位置由静止释放，与小球m₂相碰，并且多次重复．
接下来要完成的必要步骤是                    ．(填选项前的符号)
A．用天平测量两个小球的质量m₁、m₂ ；
B．测量小球m₁开始释放高度h ；
C．测量抛出点距地面的高度H ；
D．分别找到m₁、m₂相碰后平均落地点的位置M、N ；
E．测量平抛射程OM，ON .
（3）. （4分）若两个小球相碰前后的动量守恒，其表达式可以表示为             。[利用（2）中所测量的物理量表示]；若碰撞是弹性的碰撞，那么还应该满足的表达式应该为                  。[利用（2）中所测量的物理量表示]．

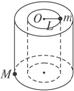
图7

（1）绳断裂瞬间小球的速度v；

（2）圆柱形薄壳半径R.

A.1∶2          B.1∶1            C.2∶1             D.1∶4

图7