
题目列表(包括答案和解析)
 如图甲所示,一个半径r=10cm圆盘由两种材料Ⅰ、Ⅱ构成,每种材料正好形成一个半圆,它们之间除圆心O以外由绝缘薄膜隔开.圆盘下端浸没在导电液体中,O点到液面的距离是半径r的
如图甲所示,一个半径r=10cm圆盘由两种材料Ⅰ、Ⅱ构成,每种材料正好形成一个半圆,它们之间除圆心O以外由绝缘薄膜隔开.圆盘下端浸没在导电液体中,O点到液面的距离是半径r的
| ||
| 2 |
| q |
| m |
| 2 |
| 3 |
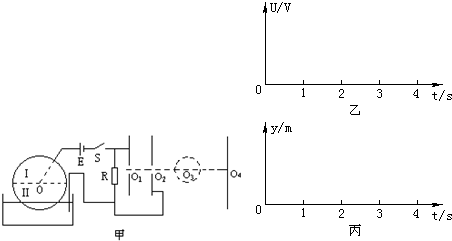
 倍.圆盘可绕O点按顺时针方向转动,且在转动过程中,只要材料进入液体中,材料Ⅰ在O点与液体间的电阻恒为RⅠ=1kΩ,材料Ⅱ在O点与液体间的电阻恒为RⅡ=4kΩ.圆盘通过转轴、导电液体与外电路连接,导线与导电液体电阻不计.电路中电源电动势E=2000V,内阻不计,R=4kΩ.R的两端与两块竖直放置、正对且等大的平行金属板相连,板间距离不计.金属板右侧依次有半径为r/10的圆形匀强磁场区域及竖直放置的荧光屏,已知平行金属板正中央的小孔O1、O2,匀强磁场的圆心O3,荧光屏的中心O4在同一条水平直线上,O3O4=20cm.现有一细束带电粒子从O1点沿O1O2方向进入平行金属板间,初速度及重力不计,比荷
倍.圆盘可绕O点按顺时针方向转动,且在转动过程中,只要材料进入液体中,材料Ⅰ在O点与液体间的电阻恒为RⅠ=1kΩ,材料Ⅱ在O点与液体间的电阻恒为RⅡ=4kΩ.圆盘通过转轴、导电液体与外电路连接,导线与导电液体电阻不计.电路中电源电动势E=2000V,内阻不计,R=4kΩ.R的两端与两块竖直放置、正对且等大的平行金属板相连,板间距离不计.金属板右侧依次有半径为r/10的圆形匀强磁场区域及竖直放置的荧光屏,已知平行金属板正中央的小孔O1、O2,匀强磁场的圆心O3,荧光屏的中心O4在同一条水平直线上,O3O4=20cm.现有一细束带电粒子从O1点沿O1O2方向进入平行金属板间,初速度及重力不计,比荷 .匀强磁场的磁感应强度B=1.0T,圆盘的转动周期T=4s.
.匀强磁场的磁感应强度B=1.0T,圆盘的转动周期T=4s.
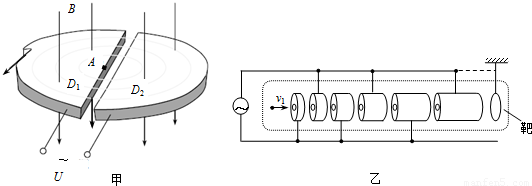

1932年,劳伦斯和利文斯设计出了回旋加速器。回旋加速器的工作原理如下图(甲)所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计。磁感应强度为B的匀强磁场与盒面垂直。A处粒子源产生的粒子,质量为m、电荷量为+q,初速度为0,在加速器中被加速,加速电压为U。加速过程中不考虑相对论效应和重力作用。
(1)求粒子第1次和第2次经过两D形盒间狭缝后轨道半径之比;
(2)求粒子从静止开始加速到出口处所需的时间t和粒子获得的最大动能Ekm;
(3)近年来,大中型粒子加速器往往采用多种加速器的串接组合。例如由直线加速器做为预加速器,获得中间能量,再注入回旋加速器获得最终能量。n个长度逐个增大的金属圆筒和一个靶,它们沿轴线排列成一串,如图(乙)所示(图中只画出了六个圆筒,作为示意)。各筒相间地连接到频率为f、最大电压值为U的正弦交流电源的两端。整个装置放在高真空容器中。圆筒的两底面中心开有小孔。现有一电量为q、质量为m的正离子沿轴线射入圆筒,并将在圆筒间的缝隙处受到电场力的作用而加速(设圆筒内部没有电场)。缝隙的宽度很小,离子穿过缝隙的时间可以不计。已知离子进入第一个圆筒左端的速度为v1,且此时第一、二两个圆筒间的电势差![]() 1-
1-![]() 2=-U。为为使打到靶上的离子获得最大能量,各个圆筒的长度应满足什么条件?并求出在这种情况下打到靶上的离子的能量。
2=-U。为为使打到靶上的离子获得最大能量,各个圆筒的长度应满足什么条件?并求出在这种情况下打到靶上的离子的能量。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com