练习册

  • 练习册
  • 试题
    如右图所示为一小球做平抛运动的闪光照片的一部分.图中背景方格的边长为5cm.如果取g=10m/s2.则: (1)闪光的频率是 Hz, (2)小球做平抛运动时的初速度大小是 m／s, (3)小球经过B点时的速度大小是 m／s. 【查看更多】

     

    题目列表(包括答案和解析)

    如右图所示为一小球做平抛运动的闪光照相照片的后面一部分，图中背景方格的边长均为4.8 cm，闪光频率是10Hz，那么，（1）小球运动中水平分速度的大小是________　m/s;（2）所在地的重力加速度是         m/s2；（3）小球经过B点时的速度大小是__     ______　m/s.

    查看答案和解析>>

    如右图所示，光滑斜面的倾角为θ，若将一小球在斜面上离底边长L处沿斜面水平方向以速度v0抛出，问小球滑到斜面底端时位移s是多大？末速度vt多大？
    某同学对此题的解法为：
    平抛出的小球下落高度为Lsinθ，位移为s，则有Lsinθ=
    1
    2
    gt2    ，s=v0t，vt=
    v
    2
    0
    +(gt)2
    ．
    由此可求得位移s和末速度vt．
    问：你同意上述解法吗？若同意，求出位移s和末速度vt；若不同意，则说明理由并求出你认为正确的结果．
    有错误．
    错因：小球所做的不是平抛运动，而是类平抛运动．
    正解：小球在斜面内的运动情况是：水平方向上，以初速度v0做匀速直线运动；在沿斜面向下的方向上，以加速度a=gsinθ做初速度为零的匀加速直线运动．其运动轨迹为抛物线，称为类平抛运动．
    依运动的独立性及等时性有：L=
    1
    2
    gsinθ?t2    t=
    2L
    gsinθ
    s=
    		(v0t)2+L2
    =
    2
    v
    2
    0
    L
    g?sinθ
    +L2
    vt=
    v
    2
    0
    +(gsinθ?t)2

    ∴s=v0
    2L
    g?sinθ
    vt=
    v
    2
    0
    +2gLsinθ
    ．

    查看答案和解析>>

    如右图所示，长度为L、内壁光滑的细直管与水平地面成30°角固定放置．将一质量为m的小球固定在管底，用一轻质光滑细线将小球与质量为M＝km的小物块相连，小物块悬挂于管口．现将小球释放，一段时间后，小物块落地静止不动，小球继续向上运动，通过管口的弯口转向装置后做平抛运动，小球在转向过程中速率不变，管内细线可视为与细直管平行，小球和小物块均可视为质点．（重力加速度为g）

    ⑴试求：小物块下落过程中的加速度大小；

    ⑵试求：小球从管口抛出时的速度大小；

    ⑶试证明：小球平抛运动的水平位移总小于．

     

    查看答案和解析>>

    如右图所示，长度为L、内壁光滑的细直管与水平地面成30°角固定放置．将一质量为m的小球固定在管底，用一轻质光滑细线将小球与质量为M＝km的小物块相连，小物块悬挂于管口．现将小球释放，一段时间后，小物块落地静止不动，小球继续向上运动，通过管口的弯口转向装置后做平抛运动，小球在转向过程中速率不变，管内细线可视为与细直管平行，小球和小物块均可视为质点．（重力加速度为g）
    ⑴试求：小物块下落过程中的加速度大小；
    ⑵试求：小球从管口抛出时的速度大小；
    ⑶试证明：小球平抛运动的水平位移总小于．

    查看答案和解析>>

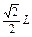    如右图所示，宇航员站在某质量分布均匀的星球表面一斜坡上P点沿水平方向以初速度v0抛出一个小球，测得小球经时间t落到斜坡上另一点Q，斜面的倾角为α，已知该星球半径为R，万有引力常量为G，求：

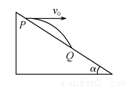
    (1)该星球表面的重力加速度；       

    (2)该星球的密度；

    (3)该星球的第一宇宙速度；         

    (4)人造卫星绕该星球做匀速圆周运动的最小周期．

     

    查看答案和解析>>


    同步练习册答案