
题目列表(包括答案和解析)
课堂上老师给同学们布置了这样一个题目:假设地球是一半径为R,质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。求矿井底部和地球表面处的重力加速度大小之比。李明同学的思考过程如下: 由等式GM=gR2(G为引力常量,M为地球质量,R为地球半径,g为地球表面处的重力加速度)变形后得到 ,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比
,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比 。下列说法中正确的是
。下列说法中正确的是
A.李明的答案是正确的
B.李明的答案是错误的,因为等式GM=gR2不成立
C.李明的答案是错误的,因为本题不能用等式GM=gR2求解
D.李明的答案是错误的,本题虽然能用等式GM=gR2求解,但他分析问题时出现错误
课堂上老师给同学们布置了这样一个题目:假设地球是一半径为R,质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。求矿井底部和地球表面处的重力加速度大小之比。李明同学的思考过程如下: 由等式GM=gR2(G为引力常量,M为地球质量,R为地球半径,g为地球表面处的重力加速度)变形后得到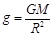 ,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比
,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比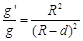 。下列说法中正确的是
。下列说法中正确的是
| A.李明的答案是正确的 |
| B.李明的答案是错误的,因为等式GM=gR2不成立 |
| C.李明的答案是错误的,因为本题不能用等式GM=gR2求解 |
| D.李明的答案是错误的,本题虽然能用等式GM=gR2求解,但他分析问题时出现错误 |
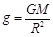 ,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比
,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比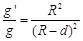 。下列说法中正确的是
。下列说法中正确的是| A.李明的答案是正确的 |
| B.李明的答案是错误的,因为等式GM=gR2不成立 |
| C.李明的答案是错误的,因为本题不能用等式GM=gR2求解 |
| D.李明的答案是错误的,本题虽然能用等式GM=gR2求解,但他分析问题时出现错误 |
课堂上老师给同学们布置了这样一个题目: 假设地球是一半径为R,质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。求矿井底部和地球表面处的重力加速度大小之比。
李明同学的思考过程如下:由等式GM=gR2(G为引力常量,M为地球质量,R为地球半径,g为地球表面处的重力加速度)变形后得到![]() ,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比
,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比![]() 。
。
下列说法中正确的是
A.李明的答案是正确的
B.李明的答案是错误的,因为等式GM=gR2不成立
C.李明的答案是错误的,因为本题不能用等式GM=gR2求解
D.李明的答案是错误的,本题虽然能用等式GM=gR2求解,但他分析问题时出现错误
课堂上老师给同学们布置了这样一个题目:
假设地球是一半径为R,质量分布均匀的球体。一矿井深度为d。已知质量分布均匀的球壳对壳内物体的引力为零。求矿井底部和地球表面处的重力加速度大小之比。
李明同学的思考过程如下:
由等式GM=gR2(G为引力常量,M为地球质量,R为地球半径,g为地球表面处的重力加速度)变形后得到![]() ,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比
,则矿井底部的重力加速度g′与地球表面处的重力加速度g大小之比![]() 。
。
下列说法中正确的是
A.李明的答案是正确的
B.李明的答案是错误的,因为等式GM=gR2不成立
C.李明的答案是错误的,因为本题不能用等式GM=gR2求解
D.李明的答案是错误的,本题虽然能用等式GM=gR2求解,但他分析问题时出现错误
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com