练习册

  • 练习册
  • 试题
    如图8所示:A和B之间的距离为L.电子在A点的速度v0 (1)要使电子沿半圆周由A运动到B.求所加匀强磁场的磁感应强度的大小和方向, (2)电子从A运动到B需要多长时间? 【查看更多】

     

    题目列表(包括答案和解析)

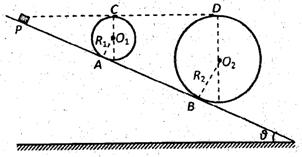
    如图所示是游乐场中过山车的模型图，图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道，固定在倾角为θ=37°斜轨道面上的A、B两点，且两圆形轨道的最高点C、D均与P点平齐，圆形轨道与斜轨道之间圆滑连接，现使小车（视为质点）从P点以一定的初速度沿斜面向下运动，已知斜轨道面与小车间的动摩擦因数为μ=
    16
    ，g=10m/s2，sin37°=0.6，cos37°=0.8．问：
    （1）若小车恰能通过第一个圆形轨道韵最高点C，则在C点速度多大？PA距离多人？
    （2）若小车恰好能通过第一个圆形轨道的最高点C，P点的初速度应为多大？
    （3）若小车在P点的初速度为15m/s，则小车能否安全通过两个圆形轨道？

    查看答案和解析>>

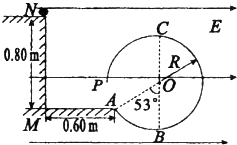    精英家教网如图所示，光滑绝缘水平台距水平地面高h=0.80m，地面与竖直绝缘光滑圆形轨道在A 点连接．A点距竖直墙壁s=0.60m，整个装置位于水平向右的匀强电场中．现将质量为m=0.1kg、电荷量为g=1×10-3C的带正电荷的小球（可视为质点），从平台上的端点N由静止释放，离开平台N点后恰好切入半径为R=0.4m的绝缘光滑圆形轨道，并沿圆形轨道运动到P点射出．图中O点是圆轨道的圆心，B、C分别是圆形轨道的最低点和最高点．AO与BO之间夹角为53°，取g=10m/s2，sin37°=0.6，cos37°=0.8．求：
    （1）电场强度E的大小；
    （2）运动过程中，电场力做正功最多时的速度（结果可以保留根式）．

    查看答案和解析>>

    如图所示是游乐场中过山车的模型图，图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道，固定在倾角为斜轨道面上的A、B两点，且两圆形轨道的最高点C、D均与P点平齐，圆形轨道与斜轨道之间圆滑连接，现使小车（视为质点）从P点以一定的初速度沿斜面向下运动，已知斜轨道面与小车间的动摩擦因数为= 1/6，g= 10m/s2，。问：

       （1）若小车恰能通过第一个圆形轨道韵最高点C，则在C点速度多大？PA距离多人？

       （2）若小车恰好能通过第一个圆形轨道的最高点C，P点的初速度应为多大？

       （3）若小车在P点的初速度为15m/s，则小车能否安全通过两个圆形轨道？

    查看答案和解析>>

    如图所示，摩托车做腾跃特技表演，以1.0m／s的初速度沿曲面冲上高0.8m、顶部水平的高台，若摩托车冲上高台的过程中始终以额定功率1.8kW行驶，经过1.2s到达平台顶部，立即关闭油门，离开平台后，恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道，并沿轨道下滑．A、B为圆弧两端点，圆弧的最低点B与水平传送带相切,传送带以v1=8m/s的速度匀速运动,传送带长为8.5m，摩托车轮胎与传送带间为滑动摩擦,动摩擦因数为μ=0.4。已知圆弧半径为R=m，AB所对应的圆心角为θ=53o，人和车的总质量为180kg，特技表演的过程中到达传送带之前不计一切阻力(计算中取g=10m／s2，)。求：  

    (1)人和车到达顶部平台时的速度v；

    (2)从平台飞出到A点，人和车运动的水平距离s；

    (3) 人和车运动到圆弧轨道最低点O时对轨道的压力；

    (4) 人和车在传送带上的运动时间。

     

    查看答案和解析>>

    如图所示是游乐场中过山车的模型图，图中半径分别为R1=2.0m和R2=8.0m的两个光滑圆形轨道，固定在倾角为斜轨道面上的A、B两点，且两圆形轨道的最高点C、D均与P点平齐，圆形轨道与斜轨道之间圆滑连接，现使小车（视为质点）从P点以一定的初速度沿斜面向下运动，已知斜轨道面与小车间的动摩擦因数为= 1/6，g=10m/s2，。问：

       （1）若小车恰能通过第一个圆形轨道韵最高点C，则在C点速度多大？PA距离多人？

       （2）若小车恰好能通过第一个圆形轨道的最高点C，P点的初速度应为多大？

       （3）若小车在P点的初速度为15m/s，则小车能否安全通过两个圆形轨道？

     

    查看答案和解析>>


    同步练习册答案