
题目列表(包括答案和解析)
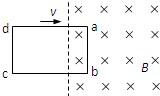 在光滑绝缘水平面上,一个电阻为0.1Ω、质量为0.05kg的矩形金属框abcd以10m/s的初速度滑进一匀强磁场,ab边长0.1m,如图所示为俯视图.匀强磁场的磁感应强度B为0.5T,方向竖直向下,范围足够大.当金属框有一部分滑进磁场,产生了1.6J的热量时,对金属框施加一垂直于ab边的水平外力,使它开始做匀减速运动(计为t=0时刻),第3s末使金属框的速度变为零,此时cd边仍在磁场外.则t=1s时,水平外力F的大小是
在光滑绝缘水平面上,一个电阻为0.1Ω、质量为0.05kg的矩形金属框abcd以10m/s的初速度滑进一匀强磁场,ab边长0.1m,如图所示为俯视图.匀强磁场的磁感应强度B为0.5T,方向竖直向下,范围足够大.当金属框有一部分滑进磁场,产生了1.6J的热量时,对金属框施加一垂直于ab边的水平外力,使它开始做匀减速运动(计为t=0时刻),第3s末使金属框的速度变为零,此时cd边仍在磁场外.则t=1s时,水平外力F的大小是

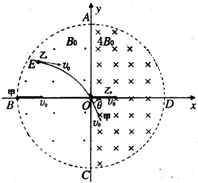 光滑绝缘水平面上有甲、乙、丙三个很小的金属球,质量均为m,甲不带电,乙带电量为+q,丙带电量为+
光滑绝缘水平面上有甲、乙、丙三个很小的金属球,质量均为m,甲不带电,乙带电量为+q,丙带电量为+| 1 |
| 2 |
| mv0 |
| qB0 |
| π |
| 3 |
| 1 |
| 2 |
 |
| EO |
 |
| ADC |
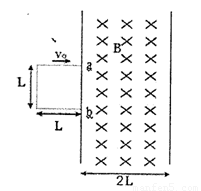
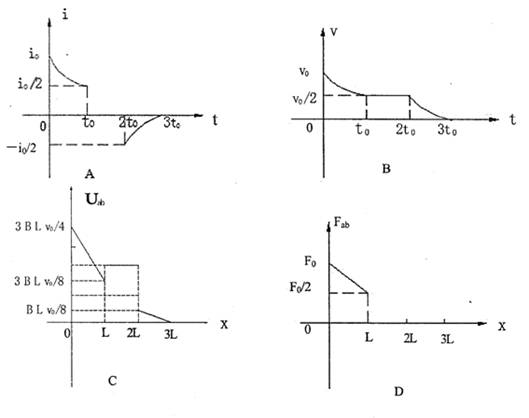
光滑绝缘水平面上存在竖直向下的匀强磁场B,宽度为2L,一边长为L、电阻为R.用同种材料做成的正方形线框以初速度v0从左侧冲进磁场区域,俯视图如图21 -(a)所示,当线框完全离开磁场时速度恰好为零.以ab边刚进入磁场时为时间和位移的零点,用v表示线框速度(以右为正方向),i表示回路中的感应电流(以逆时针方向为正,i0表示零时刻回路的感应电流),Uab表示a、b两点间的电压,Fab表示ab边所受的安培力(向左为正,F0表示零时刻ab边所受的安培力).则关于以上四个物理量对时间t或对位移x的图象中正确的是( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com