
题目列表(包括答案和解析)
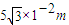 的空间有垂直纸面向里的匀强磁场,磁感应强度B=4×10-3T,在y≤0空间同时存在沿y轴负方向的匀强电场,电场强度E=
的空间有垂直纸面向里的匀强磁场,磁感应强度B=4×10-3T,在y≤0空间同时存在沿y轴负方向的匀强电场,电场强度E= .一个质量m=6.4×10-27kg、带电量g=十3.2×10-19C的带电粒子以初速度v.=2×104m/s从y轴上的P点(纵坐标为
.一个质量m=6.4×10-27kg、带电量g=十3.2×10-19C的带电粒子以初速度v.=2×104m/s从y轴上的P点(纵坐标为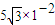 m)出发,沿着一y方向进入区域I.粒子重力不计,粒子在整个运动过程中始终没有穿出电磁场区域.
m)出发,沿着一y方向进入区域I.粒子重力不计,粒子在整个运动过程中始终没有穿出电磁场区域.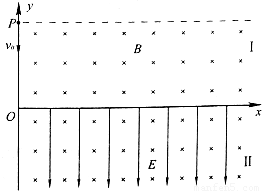
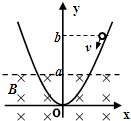 如图所示,在竖直平面有一个形状为抛物线的光滑轨道,其下半部分处在一个垂直纸面向里的非匀强磁场中,磁场的上边界是y=a的直线(图中虚线所示).一个小金属环从轨道上y=b(b>a)处以速度v沿轨道下滑,则:首次到达y=a进入磁场瞬间,小金属环中感应电流的方向为
如图所示,在竖直平面有一个形状为抛物线的光滑轨道,其下半部分处在一个垂直纸面向里的非匀强磁场中,磁场的上边界是y=a的直线(图中虚线所示).一个小金属环从轨道上y=b(b>a)处以速度v沿轨道下滑,则:首次到达y=a进入磁场瞬间,小金属环中感应电流的方向为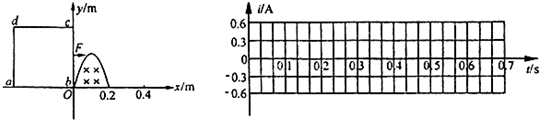
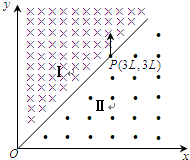 如图所示,在空间中有一坐标系oxy,其第一象限中充满着两个方向不同的匀强磁场区域Ⅰ和Ⅱ.直线OP是它们的边界.区域Ⅰ中的磁感应强度为2B,方向垂直纸面向内,区域Ⅱ中的磁感应强度为B,方向垂直纸面向外,边界上的P点坐标为(3L,3L).一质量为m,电荷量为+q的粒子从P点平行于y轴正方向以速度v0=
如图所示,在空间中有一坐标系oxy,其第一象限中充满着两个方向不同的匀强磁场区域Ⅰ和Ⅱ.直线OP是它们的边界.区域Ⅰ中的磁感应强度为2B,方向垂直纸面向内,区域Ⅱ中的磁感应强度为B,方向垂直纸面向外,边界上的P点坐标为(3L,3L).一质量为m,电荷量为+q的粒子从P点平行于y轴正方向以速度v0=| 2BqL | m |
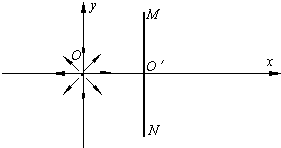 如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右边有一很薄的挡板,挡板与xoy平面交线的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为q,速度为υ,MN的长度为L.(不计带电粒子的重力)
如图所示,在直角坐标系的原点O处有一放射源,向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子.在放射源右边有一很薄的挡板,挡板与xoy平面交线的两端M、N与原点O正好构成等腰直角三角形.已知带电粒子的质量为m,带电量为q,速度为υ,MN的长度为L.(不计带电粒子的重力)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com