
题目列表(包括答案和解析)
 如图所示,相邻两车站间距相等,在一条直线上.车在两站间行驶时平均速度均为v车,每次靠站停顿时间均为t.某同学位于车站1与车站2之间离车站2较近的某一位置,当车从车站3开动的同时,他向车站2以平均速度v人奔跑,并恰能赶上汽车,车长不计.
如图所示,相邻两车站间距相等,在一条直线上.车在两站间行驶时平均速度均为v车,每次靠站停顿时间均为t.某同学位于车站1与车站2之间离车站2较近的某一位置,当车从车站3开动的同时,他向车站2以平均速度v人奔跑,并恰能赶上汽车,车长不计.如图所示,相邻两车站间距相等,在一条直线上. 车在两站间行驶时平均速度均为v车,每次靠站停顿时间均为t. 某同学位于车站1与车站2之间离车站2较近的某一位置,当车从车站3开动的同时,他向车站2以平均速度v人奔跑,并恰能在汽车离站前赶上汽车,车长不计. 于是该同学得出结论:若他仍以此平均速度从原位置向车站1奔跑,也一定能赶得上这辆班车.
|
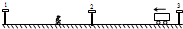 如图所示,相邻两车站间距相等,在一条直线上.车在两站间行驶时平均速度均为v车,每次靠站停顿时间均为t.某同学位于车站1与车站2之间离车站2较近的某一位置,当车从车站3开动的同时,他向车站2以平均速度v人奔跑,并恰能赶上汽车,车长不计.
如图所示,相邻两车站间距相等,在一条直线上.车在两站间行驶时平均速度均为v车,每次靠站停顿时间均为t.某同学位于车站1与车站2之间离车站2较近的某一位置,当车从车站3开动的同时,他向车站2以平均速度v人奔跑,并恰能赶上汽车,车长不计.
|

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com