
题目列表(包括答案和解析)
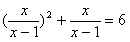 的步骤如下:
的步骤如下: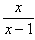 =y,则原方程化为y2+y=6,解这个方程,得y1= -3,y2=2
=y,则原方程化为y2+y=6,解这个方程,得y1= -3,y2=2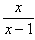 = -3 ,∴x= -3x+3,∴x1=
= -3 ,∴x= -3x+3,∴x1=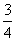
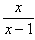 =2, ∴x=2x-2,∴x2=2
=2, ∴x=2x-2,∴x2=2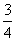 ,x2=2都是原方程的根。以上各步骤中,所有的正确的步骤是
,x2=2都是原方程的根。以上各步骤中,所有的正确的步骤是  ,我们可以将x2-1视为一个整体,设x2-1=y
,我们可以将x2-1视为一个整体,设x2-1=y


 元交费。下表是该地区一户居民10月份、11月份的用电情况。根据表中的数据,求在该地区规定的电费计费方式中,a度用电量为多少?
元交费。下表是该地区一户居民10月份、11月份的用电情况。根据表中的数据,求在该地区规定的电费计费方式中,a度用电量为多少? 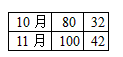
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com