
题目列表(包括答案和解析)
问题提出:
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小. 而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形. 并利用差的符号来确定它们的大小,即耍比较代数式 M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0;则 M<N.
问题解决:
如图①.把边长为 a+b(a≠b)的大正方形分割成两个边长分别是 a、b 的小正方形及两个矩形,试比较两个小正方形的面积之和 M与两个矩形面积之和N 的大小.类比应用:
(1)已知小丽和小颖购买同一种商品的平均价格分别为 元/千克、
元/千克、 元/千克(a·b是正数.且a≠b),试比较小丽和小颖所购商品的平均价格的高低.
元/千克(a·b是正数.且a≠b),试比较小丽和小颖所购商品的平均价格的高低.
(2)试比技图②、图③两个矩形的周长 M, 、N, 的大小(b>c).



 ,PC=1.求∠BPC度数的大小和等边三角形ABC的边长.
,PC=1.求∠BPC度数的大小和等边三角形ABC的边长. .问题得到解决.?
.问题得到解决.? ,BP=
,BP= ,PC=1.求∠BPC度数的大小和正方形ABCD的边长.
,PC=1.求∠BPC度数的大小和正方形ABCD的边长.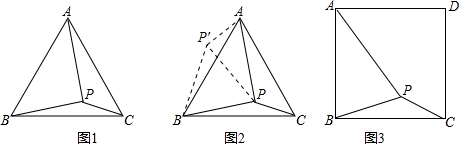
 式子
式子 可以理解为“以a、b为直角边长的直角三角形的斜边长”,利用这个知识,我们可以恰当地构造图形来解决一些数学问题.比如在解“已知a+b=2,则
可以理解为“以a、b为直角边长的直角三角形的斜边长”,利用这个知识,我们可以恰当地构造图形来解决一些数学问题.比如在解“已知a+b=2,则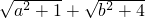 的最小值为________”时,我们就可以构造两个直角三角形,转化为“求两个直角三角形的斜边和最小是多少”的问题.请你根据所给图形和题意,在横线上填上正确的答案.
的最小值为________”时,我们就可以构造两个直角三角形,转化为“求两个直角三角形的斜边和最小是多少”的问题.请你根据所给图形和题意,在横线上填上正确的答案.我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题: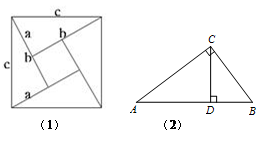
(1)如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,请你用它来验证勾股定理;
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC= 4,BC=3,求CD的长度.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com