
题目列表(包括答案和解析)
过点P(1,0)作曲线C:![]() 的切线,切点为Q1,设Q1在
的切线,切点为Q1,设Q1在![]() 轴上的投影是Pl,又过P1作曲线C的切线,切点为Q2,设Q2在
轴上的投影是Pl,又过P1作曲线C的切线,切点为Q2,设Q2在![]() 轴上的投影是P2,……依次下去,得到一系列Q1、Q2、…、Q
轴上的投影是P2,……依次下去,得到一系列Q1、Q2、…、Q![]() ,设点Q
,设点Q![]() 横坐标为
横坐标为![]() .
.
(1)求![]() 的值,并求出
的值,并求出![]() 与
与![]() 的关系;
的关系;
(2)令![]() ,设数列{
,设数列{![]() }的前
}的前![]() 项和为
项和为![]() ,求
,求![]() .
.
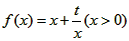 ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N,
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N,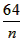 ]内,总存在m+1个数a1,a2,....,am,
]内,总存在m+1个数a1,a2,....,am,已知函数![]() ,过点P(1,0)作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
,过点P(1,0)作曲线y=f(x)的两条切线PM、PN,切点分别为M、N.
(1)当t=2时,求函数f(x)的单调递增区间;
(2)设|MN|=g(t),试求函数g(t)的表达式
(3)在(2)的条件下,若对任意的正整数n,在区间[![]() ]内总存在m+1个实数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
]内总存在m+1个实数a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
已知函数![]() ,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
,过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N.
(1)当t=2时,求函数f(x)的单调递增区间;
(2)设|MN|=g(t),试求函数g(t)的解析式;
(3)在(2)的条件下,若对任意的正整数n,在区间![]() 内总存在m+1个实数λ1,λ2……λm,λm+1使得不等式g(λ1)+g(λ2)+…+g(λm)<g(λm+1)成立,求m的最大值.
内总存在m+1个实数λ1,λ2……λm,λm+1使得不等式g(λ1)+g(λ2)+…+g(λm)<g(λm+1)成立,求m的最大值.
| n |
| k+1 |
| n |
 |
| i=0 |
| a | 2 n-i |
| C | i 2n-i+1 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com