
题目列表(包括答案和解析)
三、解答题:本大题共6小题,共80分.
15.(本小题满分13分)
已知函数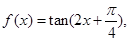 ,
,
(Ⅰ)求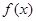 的定义域与最小正周期;
的定义域与最小正周期;
(Ⅱ)设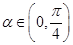 ,若
,若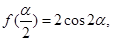 求
求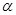 的大小.
的大小.
三、解答题:本大题共6小题,共80分.
15.(本小题满分13分)
已知函数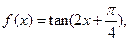 ,
,
(Ⅰ)求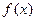 的定义域与最小正周期;
的定义域与最小正周期;
(Ⅱ)设 ,若
,若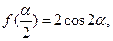 求
求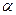 的大小.
的大小.
| 4 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
(本小题满分12分)
甲乙两个班级进行一门课程的考试,按照学生考试成绩优秀和不优秀统计成绩后,得到如下的列联表:
班级与成绩列联表
|
|
优 秀 |
不优秀 |
|
甲 班 |
10 |
35 |
|
乙 班 |
7 |
38 |
根据列联表的独立性检验,能否在犯错误的概率不超过0.01的前提下认为成绩与班级有关系?
附:
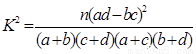
|
|
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分15分)
在平面直角坐标系中,已知点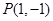 ,过点
,过点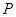 作抛物线
作抛物线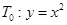 的切线,其切点分别为
的切线,其切点分别为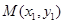 、
、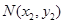 (其中
(其中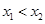 ).
).
(1)求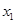 与
与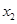 的值;
的值;
(2)若以点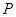 为圆心的圆
为圆心的圆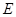 与直线
与直线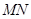 相切,求圆
相切,求圆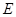 的面积;
的面积;
(3)过原点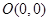 作圆
作圆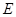 的两条互相垂直的弦
的两条互相垂直的弦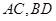 ,求四边形
,求四边形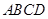 面积的最大值.
面积的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com