
题目列表(包括答案和解析)
设a、b为常数,M={f(x)|f(x)=acosx+bsinx};F:把平面上任意一点(a,b)映射为函数acosx+bsinx.
(1)证明:不存在两个不同点对应于同一个函数;
(2)证明:当f0(x)∈M时,f1(x)=f0(x+t)∈M,这里t为常数;
(3)对于属于M的一个固定值f0(x),得M1={f0(x+t),t∈R},在映射F的作用下,M1作为象,求其原象,并说明它是什么图象?
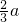 ,P到一条准线的距离是
,P到一条准线的距离是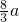 ,则此椭圆的离心率为
,则此椭圆的离心率为 .
. (a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|为定值.
(a≠b,且a,b为正的常数)的准线上任意一点到两焦点的距离分别为d1,d2,则|d12-d22|为定值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com