(13)设函数.则其导函数展开式中的系数是 ▲ . (14)数列的前n项和.则= ▲ . (15)在直角坐标系中.已知点A.且AC⊥BC.|AC|=2|BC|.则C点的横坐标为 ▲ . (16)已知某游乐园内摩天轮的中心O点距地面的高度为50m.摩天轮做匀速转动.摩天轮上的一点P自最低点A点起.经过t min后.点P的高度.那么在摩天轮转动一圈的过程中.点P的高度在距地面70m以上的时间将持续 ▲ min. .三.解答题:本大题6个小题.共74分.解答必需写出必要的文字说明.推理过程或计算步骤. 已知向量a=().b=().c=.d=(0.1). (1)求证:a⊥(b+c), (2)设 a·(b- d).且.求的值域. 某电视台游戏节目想利用若干大小.形状相同的小球设计一个摸球的抽奖游戏.游戏者要连过两关才能赢得大奖.第一关:在一个放有3个红球和7个白球的暗箱中.一次摸取三个球.若摸出的球中有红球.即可过关.第二关:在与第一关相同的暗箱中.一次摸取三个球.若摸出的三个球恰好同色.即可过关. (1)求第一关过关的概率, (2)求赢得大奖的概率. 在正四棱柱中.. P为BC的中点. (1)求直线AC与平面ABP所成的角, (2)求异面直线AC与BP所成的角, (3)求点B到平面APC的距离. 已知双曲线的左顶点为A.右焦点为F.过点F作垂直于x轴的直线与双曲线交于B.C两点.且AB⊥AC.|BC|=6. (1)求双曲线的方程, (2)设过点F且不垂直于x轴的直线l与双曲线分别交于点P.Q.请问:是否存在直线l.使△APQ构成以A为直角顶点的等腰直角三角形?若存在.求出所有满足条件的直线l的方程,若不存在.请说明理由. A城市的出租车计价方式为:若行程不超过3千米.则按“起步价 10元计价,若行程超过3千米.则之后2千米以内的行程按“里程价 计价.单价为1.5元/千米,若行程超过5千米.则之后的行程按“返程价 计价.单价为2.5元/千米.设某人的行程为x千米.现有两种乘车方案:①乘坐一辆出租车,②每5千米换乘一辆出租车. (1)分别写出两种乘车方案计价的函数关系式, (2)对不同的出行行程.①②两种方案中哪种方案的价格较低?请说明理由. 已知函数在区间[n.m]上为减函数.记m的最大值为m0.n的最小值为n 0.且有m0- n 0=4. (1)求m0.n 0的值以及函数的解析式, (2)已知等差数列{xn}的首项.公差.又过点 的直线方程为试问:在数列{xn}中.哪些项满足? (3)若对任意.都有成立.求a的最小值. 【
查看更多】
题目列表(包括答案和解析)
给出以下四个命题:
①动点

到两定点

的距离之和为4,则点

的轨迹为椭圆;
②设定义在

上的可导函数

满足

,

,则

一定成立;
③

展开式中,含

项的系数为30;
④若

,则

.
其中,所有真命题的序号为 .
查看答案和解析>>

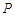 到两定点
到两定点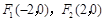 的距离之和为4,则点
的距离之和为4,则点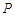 的轨迹为椭圆;
的轨迹为椭圆;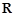 上的可导函数
上的可导函数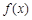 满足
满足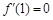 ,
, ,则
,则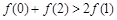 一定成立;
一定成立;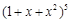 展开式中,含
展开式中,含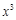 项的系数为30;
项的系数为30;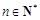 ,则
,则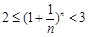 .
. 到两定点
到两定点 的距离之和为4,则点
的距离之和为4,则点 的轨迹为椭圆;
的轨迹为椭圆; 上的可导函数
上的可导函数 满足
满足 ,
, ,则
,则 一定成立;
一定成立; 展开式中,含
展开式中,含 项的系数为30;
项的系数为30; ,则
,则 .
.