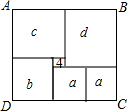如图，矩形ABCD被分成六个大小不一的正方形，已知中间一个小正方形面积为4，其他正方形的边长分别为a、b、c、d．求矩形ABCD中最大正方形与最小正方形的面积之差．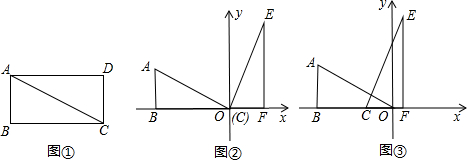

如图①，矩形ABCD被对角线AC分为两个直角三角形，AB=3，BC=6．现将Rt△ADC绕点C顺时针旋转90°，点A旋转后的位置为点E，点D旋转后的位置为点F．以C为原点，以BC所在直线为x轴，以过点C垂直于BC的直线为y轴，建立如图②的平面直角坐标系．

（1）求直线AE的解析式；
（2）将Rt△EFC沿x轴的负半轴平行移动，如图③．设OC=x（0＜x≤9），Rt△EFC与Rt△ABO的重叠部分面积为s；求当x=1与x=8时，s的值；
（3）在（2）的条件下s是否存在最大值？若存在，求出这个最大值及此时x的值；若不存在，请说明理由．

如图，矩形ABCD被两条对角线分成四个小三角形，如果四个小三角形的周长的和是86厘米，矩形的周长是30厘米，则对角线的长是厘米．

17、如图，矩形ABCD被分割成了6个边长为2的小正方形，共得到12个顶点，选取其中的三个顶点连成三角形，请回答下列问题：
（1）面积为12的锐角三角形的个数是多少？
（2）写出所有面积为10的三角形？

（2011•历下区二模）如图①，矩形ABCD被对角线AC分为两个直角三角形，AB=4，BC=8．现将Rt△ADC绕点C顺时针旋转90°，点A旋转后的位置为点M，点D旋转后的位置为点N．以C为原点，以BC所在直线为x轴，以过点C垂直于BC的直线为y轴，建立如图②的平面直角坐标系．
（1）求直线AM的解析式；
（2）将Rt△MNC沿x轴的负方向平行移动，如图③．设OC=x（0＜x≤12），Rt△MNC与Rt△ABO的重叠部分面积为S；
①当x=2与x=10时，求S的值；
②S是否存在最大值？若存在，求出这个最大值及此时x的值；若不存在，请说明理由．