练习册

  • 练习册
  • 试题
    平面内有n个圆,其中每两个圆都相交于两点,并且每三个圆都不相交于同一点,求证:n个圆把平面分成f(n)=n2-n+2个部分. 分析 本题的关键在于如何应用归纳假设及已知条件分析当n=k+1时,第k+1个圆与其他k个圆的交点个数,做到有目的的变形. 证明 (1)当n=1时,一个圆把平面分成两部分,又12-1+2=2,故命题成立. (2)假设n=k(k∈N*)时,命题成立,即满足题设条件的k个圆把平面分成f(k)=k2-k+2个部分.2分 那么当n=k+1时,设第k+1个圆为⊙O,由题意,它与k个圆中每个圆交于两点,又无三个圆交于同一点,于是它与其他k个圆交于2k个点,这些点把⊙O分成2k条弧,即f(k+1)=f(k)+2k=k2-k+2+2k=(k+1)2-(k+1)+2. 6分 这就是说,当n=k+1时,命题也成立. 综上可知,对一切n∈N*,命题都成立. 8分 【查看更多】

     

    题目列表(包括答案和解析)

    四．附加题（本小题满分8分）

    设复数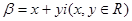与复平面上点P(x,y)对应，且复数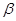满足条件

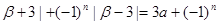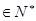    |a（其中n.常数a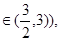当n为奇数时，动点P(x,y)的轨迹为C1, 当n为偶数时，动点P(x,y)的轨迹为C2,且两条曲线都经过点D(2,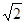),求轨迹C1  与C2的方程？

     

    查看答案和解析>>

    （09年长沙一中第八次月考理）(本小题满分12分)我校文化体育艺术节的乒乓球决赛在甲乙两人中进行，比赛规则如下：比赛采用7局4胜制（先胜4局这获胜即比赛结束），在每一局比赛中，先得11分的一方为胜方；比赛没有平局，10平后，先连得2分的一方为胜方

    （1）根据以往战况，每局比赛甲胜乙的概率为0.6，设比赛的场数为,求的分布列和期望；

    （2）若双方在每一分的争夺中甲胜的概率也为0.6，求决胜局中甲在以8:9落后的情况下最终以12:10获胜的概率。

    查看答案和解析>>


    同步练习册答案